【题目】已知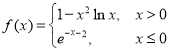
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若存在![]() 使,得关于
使,得关于![]() 的方程
的方程![]() 有三个不相同的实数根,求实数
有三个不相同的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)表示此时函数的解析式,求导分析单调性,即可求得最值.
(2)由于![]() 为分段函数,故分类讨论两段函数交点个数,将问题可转化为
为分段函数,故分类讨论两段函数交点个数,将问题可转化为![]() 的根存在三个,记
的根存在三个,记![]() ,
,![]() ,令
,令![]() ,令
,令![]() ,分两段求导分析函数图象特征,进而判定交点个数,求得参数取值范围.
,分两段求导分析函数图象特征,进而判定交点个数,求得参数取值范围.
(1)当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]()
(2)![]() ,经验证
,经验证![]() 不是方程的根,
不是方程的根,
所以原方程的根等价于![]() 的根,
的根,
记![]() ,
,![]() ,令
,令![]() ,
,![]() ,单调递减,
,单调递减,
令![]() ,即
,即![]() ,
,
令![]() 为极大值点,其在
为极大值点,其在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
当![]() ,
,![]() ,
,
所以![]() 在
在![]() 无实数根
无实数根
当![]() 时,
时,![]() ……①
……①
![]()
![]() 有两个极值点
有两个极值点![]() ,且
,且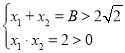 ,即
,即![]() ,
,![]()
故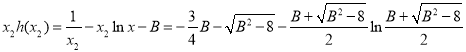
![]() 所以
所以![]() ,
,
存在![]() 使①有三个实根所以
使①有三个实根所以![]() 满足条件.
满足条件.
当![]() ,
,![]() 的分子中
的分子中![]() ,
,![]() ,显然
,显然![]() ,所以①仅有一个正根,
,所以①仅有一个正根,
要使![]() 有两个负根,则
有两个负根,则![]() ﹐
﹐
综上所![]() ﹐即
﹐即![]() .
.

