2026年小学毕业班总复习六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年小学毕业班总复习六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
例1 张师傅加工一批零件,第一天完成的个数与未完成的个数比是 $1:3$。如果再加工15个,那么就可以完成这批零件的一半。这批零件一共有多少个?
答案:
设这批零件一共有$x$个。
第一天完成的个数与未完成的个数比是$1:3$,那么第一天完成了总数的$\frac{1}{1 + 3}=\frac{1}{4}$。
可列方程:
$\frac{1}{4}x+15=\frac{1}{2}x$
移项可得:
$15=\frac{1}{2}x-\frac{1}{4}x$
$15=\frac{1}{4}x$
解得$x = 60$。
答:这批零件一共有60个。
【解析】根据“第一天完成的个数与未完成的个数比是 $1:3$”,可以得出第一天完成了总数的 $\frac{1}{4}$,再加工15个,就完成这批零件的一半,一半就是 $\frac{1}{2}$。所以15个零件占这批零件的 $\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$。本题也可以根据题意画出如下图所示的线段图:
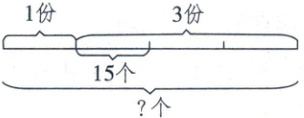
从图中,可以很清楚地得到15个零件所对应的分率是 $\frac{1}{4}$。
【答案】$15÷(\frac{1}{2}-\frac{1}{1 + 3}) = 15÷\frac{1}{4} = 60$(个)
答:这批零件一共有60个。
设这批零件一共有$x$个。
第一天完成的个数与未完成的个数比是$1:3$,那么第一天完成了总数的$\frac{1}{1 + 3}=\frac{1}{4}$。
可列方程:
$\frac{1}{4}x+15=\frac{1}{2}x$
移项可得:
$15=\frac{1}{2}x-\frac{1}{4}x$
$15=\frac{1}{4}x$
解得$x = 60$。
答:这批零件一共有60个。
【解析】根据“第一天完成的个数与未完成的个数比是 $1:3$”,可以得出第一天完成了总数的 $\frac{1}{4}$,再加工15个,就完成这批零件的一半,一半就是 $\frac{1}{2}$。所以15个零件占这批零件的 $\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$。本题也可以根据题意画出如下图所示的线段图:

从图中,可以很清楚地得到15个零件所对应的分率是 $\frac{1}{4}$。
【答案】$15÷(\frac{1}{2}-\frac{1}{1 + 3}) = 15÷\frac{1}{4} = 60$(个)
答:这批零件一共有60个。
1. 小刚和小明二人一共有零花钱250元,星期天二人一起去新华书店买书,小刚用去20元,小明用去自己钱数的20%。二人剩下的钱数之比为 $2:3$。原来他们各有多少元?
答案:
1.小明原有:$(250 - 20)×\frac{3÷(1 - 20\%)}{3÷(1 - 20\%) + 2}=$
$150(元)$
小刚原有:$250 - 150 = 100(元)$
$150(元)$
小刚原有:$250 - 150 = 100(元)$
2. 甲、乙、丙三堆煤共263吨,乙、丙两堆煤的质量比是 $5:2$,且甲堆煤比丙堆煤少7吨。甲、乙、丙三堆煤各有多少吨?
答案:
2.$(263 + 7)÷(2 + 2 + 5)=30(吨)$
丙:$30×2 = 60(吨)$
甲:$60 - 7 = 53(吨)$
乙:$30×5 = 150(吨)$
丙:$30×2 = 60(吨)$
甲:$60 - 7 = 53(吨)$
乙:$30×5 = 150(吨)$
例2 一个长方形的周长是84厘米,它的长与宽的比是 $5:2$,这个长方形的面积是多少平方厘米?
答案:
$84÷2 = 42$(厘米)
长:$42×\frac{5}{5 + 2} = 30$(厘米)
宽:$42×\frac{2}{5 + 2} = 12$(厘米)
面积:$30×12 = 360$(平方厘米)
答:这个长方形的面积是360平方厘米。
【解析】此题考查的是按比例分配的知识。想求长方形的面积,必须知道它的长与宽。已知长方形的周长及长与宽的比,可以按比例分配求出长与宽。需要注意的是这里被分配的量是长方形周长的一半。
【答案】$84÷2 = 42$(厘米)
长:$42×\frac{5}{5 + 2} = 30$(厘米)
宽:$42×\frac{2}{5 + 2} = 12$(厘米)
面积:$30×12 = 360$(平方厘米)
答:这个长方形的面积是360平方厘米。
长:$42×\frac{5}{5 + 2} = 30$(厘米)
宽:$42×\frac{2}{5 + 2} = 12$(厘米)
面积:$30×12 = 360$(平方厘米)
答:这个长方形的面积是360平方厘米。
【解析】此题考查的是按比例分配的知识。想求长方形的面积,必须知道它的长与宽。已知长方形的周长及长与宽的比,可以按比例分配求出长与宽。需要注意的是这里被分配的量是长方形周长的一半。
【答案】$84÷2 = 42$(厘米)
长:$42×\frac{5}{5 + 2} = 30$(厘米)
宽:$42×\frac{2}{5 + 2} = 12$(厘米)
面积:$30×12 = 360$(平方厘米)
答:这个长方形的面积是360平方厘米。
1. 年初,李强、张明和陈丽三人分别投资了5万元、20万元、10万元,合资办了一个股份公司。年底经过核算,公司可用于分配的利润共有3.5万元,他们三人合资时约定:“公司每年可用于分配的利润按个人出资的比例分配。”这样李强可以分得多少万元?
答案:
1.$3.5×\frac{5}{5 + 20 + 10}=0.5(万元)$
查看更多完整答案,请扫码查看


