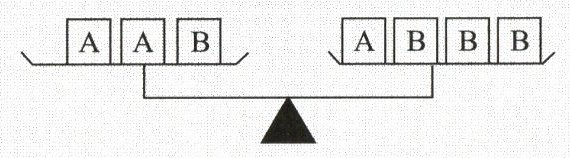
9. 如图,图中标有相同字母的物体的质量相同,若A的质量为20g,则当下图中的天平为平衡状态时,B的质量为
10
g。
答案:
9.10
10. 已知$x = 2$是关于$x$的方程$ax - 5x - 6 = 0$的解,则$a =$
8
。
答案:
10.8
11. 某市对市区主干道进行绿化,现有甲、乙两个施工队,甲施工队有13位工人,乙施工队有27位工人,现计划有变,需要从乙施工队借调$x$名工人到甲施工队,此时甲施工队人数正好是乙施工队人数的3倍,则可列方程为
13+x=3(27-x)
。
答案:
11.13+x=3(27-x)
12. 定义新运算“※”:$a※b = ab + b$。若$5※x = 12$,则$x =$
2
。
答案:
12.2
13. 一艘船从甲码头顺流而行,用了3h到达乙码头,该船从乙码头返回甲码头逆流而行,用了5h,已知水流速度是3km/h,则船在静水中的速度是
12
km/h(逆水速度=静水速度-水流速度,顺水速度=静水速度+水流速度)。
答案:
13.12
14. 如果单项式$xy^{b + 1}$与$-\frac{1}{3}x^{a + 2}y^{3}$的差是单项式,则关于$x$的方程$ax + b = 0$的解是
x=2
。
答案:
14.x=2
15. (8分)解方程:(1)$\frac{2x + 1}{3} - 1 = \frac{x + 5}{6} - \frac{2x - 3}{2}$;
(2)$\frac{4x - 1.5}{0.5} - \frac{5x - 0.8}{0.2} = \frac{1.2 - x}{0.1}$。
(2)$\frac{4x - 1.5}{0.5} - \frac{5x - 0.8}{0.2} = \frac{1.2 - x}{0.1}$。
答案:
15.解(1)去分母,得2(2x+1)-6=x+5-3(2x-3)。
去括号,得4x+2-6=x+5-6x+9。
移项,得4x-x+6x=5+9-2+6。
合并同类项,得9x=18。
系数化为1,得x=2。
(2)将分母化为整数,得$\frac{40x-15}{5}=\frac{50x-8}{2}=\frac{12-10x}{1}。$
去分母、去括号,得8x-3-25x+4=12-10x。
移项、合并同类项,得-7x=11。
系数化为1,得$x=-\frac{11}{7}。$
去括号,得4x+2-6=x+5-6x+9。
移项,得4x-x+6x=5+9-2+6。
合并同类项,得9x=18。
系数化为1,得x=2。
(2)将分母化为整数,得$\frac{40x-15}{5}=\frac{50x-8}{2}=\frac{12-10x}{1}。$
去分母、去括号,得8x-3-25x+4=12-10x。
移项、合并同类项,得-7x=11。
系数化为1,得$x=-\frac{11}{7}。$
查看更多完整答案,请扫码查看


