《2025年绩优学案八年级数学上册北师大版》

19. (5分)如图甲,笔直的公路上$A,B$两点相距20km,$C,D$为两村庄,$DA\perp AB$,垂足为$A$,$CB\perp AB$,垂足为$B$,已知$DA= 10 km,CB= 5 km$,现在计划在公路的$AB段上建一个土特产收购站E$。
(1)若规划$C,D两村到收购站E$的距离相等,则收购站$E应建在离A$点多远处？
(2)若规划$C,D两村到收购站E$的距离和最短,请在图乙中通过作图画川收购站$E$的位置,计算距离和最短为______km。

答案：
(2)25

20. (6分)甲、乙两个探测气球分别从海拔5m和15m处同时出发,匀速上升60min。如图是甲、乙两个探测气球所在位置的海拔$y$(单位：m)与气球上升时间$x$(单位：min)的函数图象。
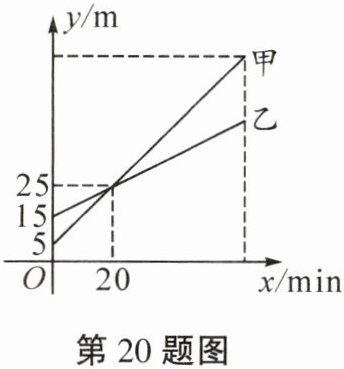
(1)求这两个气球在上升过程中$y关于x$的函数表达式；
(2)当这两个气球的海拔相差15m时,求上升的时间。

答案：
(1)设甲气球的函数表达式为$y = kx + b$,乙气球的函数表达式为$y = mx + n$。
分别将$(0,5)$,$(20,25)$和$(0,15)$,$(20,25)$代入,得$\begin{cases}5 = b\\25 = 20k + b\end{cases}$,$\begin{cases}15 = n\\25 = 20m + n\end{cases}$
解得$\begin{cases}k = 1\\b = 5\end{cases}$,$\begin{cases}m = \frac{1}{2}\\n = 15\end{cases}$
所以甲气球的函数表达式为$y = x + 5(0\leqslant x\leqslant60)$,乙气球的函数表达式为$y = \frac{1}{2}x + 15(0\leqslant x\leqslant60)$。
(2)由初始位置可得:
当$x$大于20时,两个气球的海拔可能相差$15m$,且此时甲气球海拔更高
所以$x + 5 - (\frac{1}{2}x + 15)= 15$,解得$x = 50$
所以当这两个气球的海拔相差$15m$时,上升的时间为$50min$。

21. (6分)如图,在平面直角坐标系中,点$A(0,3)和B(4,0)$。
(1)在$x轴上求点C$,使得$BA= BC$,请求出点$C$的坐标；
(2)在$y轴上求点D$,使得$\angle ABD= 90^{\circ}$,请求出点$D$的坐标。

答案：
(1)因为点$A(0,3)$,$B(4,0)$
所以$AO = 3$,$BO = 4$
所以$AB=\sqrt{OB^{2}+OA^{2}}=\sqrt{4^{2}+3^{2}}=5$
根据题意可知在$x$轴上有点$C$,使得$BA = BC$,则有两种情况,点$C$在点$B$左边时,点$C$坐标为$(-1,0)$
点$C$在点$B$右边时,点$C$的坐标为$(9,0)$
综上所述,点$C$的坐标为$(9,0)$或$(-1,0)$。
(2)设点$D(0,y)$,如图,连接$BD$,$\angle ABD = 90^{\circ}$
在$Rt\triangle ADB$和$Rt\triangle ODB$中,根据勾股定理,得$AD^{2}-AB^{2}=BD^{2}=OB^{2}+OD^{2}$
所以$(3 + OD)^{2}-5^{2}=4^{2}+OD^{2}$,解得$OD = \frac{16}{3}$
所以点$D$的坐标为$(0,\frac{16}{3})$。