7. 一次函数$y= kx+b(k\neq0)与y= bx+k(b\neq0)$在同一平面直角坐标系中的图象大致是( )
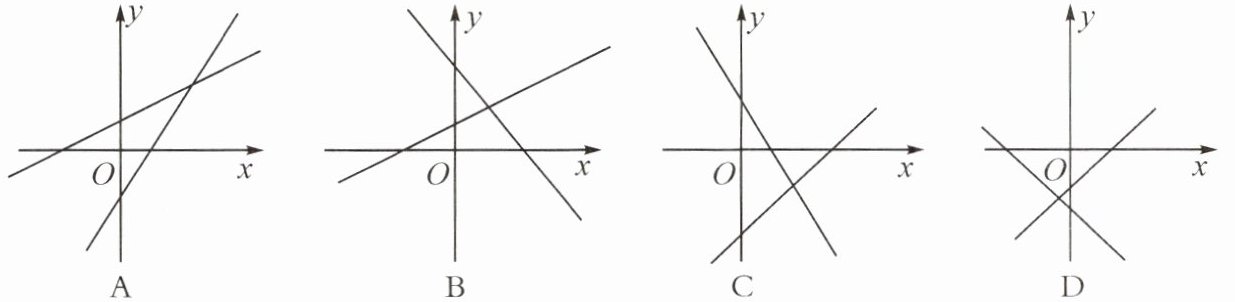

答案:
C
8. 我国古代数学的经典著作《九章算术》记载:“今有不善行者先行一十里,善行者追之一百里,先至不善行者二十里。问善行者几何里及之?”意思是:不善行者先走10里路,善行者追他,当善行者走到100里路时,超过了不善行者20里路。问善行者走到多少里路时就赶上不善行者?(“里”是我国传统长度单位)如图是善行者与不善行者行走路程$s$(单位:里)关于善行者的行走时间$t$的函数图象,则两图象交点$P$的纵坐标是( )
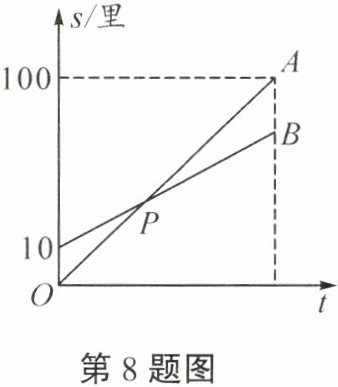
A.20
B.$\frac{80}{3}$
C.$\frac{100}{3}$
D.30

A.20
B.$\frac{80}{3}$
C.$\frac{100}{3}$
D.30
答案:
C
9. 比较大小:$\frac{\sqrt{10}}{9}$______$\frac{1}{2}$;$-\sqrt{3}$______$-\sqrt{2}$(填“$>$”“$<$”或“$=$”)。
答案:
< <
10. 已知点$A(a,2022)与点B(2023,b)关于x$轴对称,则$a+b$的值为______。
答案:
1
11. 某校有4名教师与若干名学生去看电影,电影票原价为成人每张30元,学生每张15元。现全部打8折。则打折后付款总金额$y与学生人数x$之间的函数关系式为______。
答案:
y = 12x + 96
12. 如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是______。


答案:
$\sqrt{5}$
13. 已知一次函数$y= kx+10$,当$-1\leq x\leq2$时,函数$y$的最小值是5,则$k$= ______。
答案:
5或$-\frac{5}{2}$
14. (4分)计算:
(1)$|1-\sqrt{3}|+(-\frac{1}{3})^{-1}-\sqrt{12}+(\sqrt{3}-\pi)^0$;
(2)$\sqrt{125}+9\sqrt{\frac{2}{27}}-\frac{1}{2}\sqrt{24}+(\sqrt{5})^2$。
(1)$|1-\sqrt{3}|+(-\frac{1}{3})^{-1}-\sqrt{12}+(\sqrt{3}-\pi)^0$;
(2)$\sqrt{125}+9\sqrt{\frac{2}{27}}-\frac{1}{2}\sqrt{24}+(\sqrt{5})^2$。
答案:
解:
(1)原式=$\sqrt{3}-1-3-2\sqrt{3}+1$
$=-3-\sqrt{3}$;
(2)原式=$5\sqrt{5}+9×\frac{\sqrt{6}}{9}-\frac{1}{2}×2\sqrt{6}+5$
$=5\sqrt{5}+\sqrt{6}-\sqrt{6}+5=5\sqrt{5}+5$。
(1)原式=$\sqrt{3}-1-3-2\sqrt{3}+1$
$=-3-\sqrt{3}$;
(2)原式=$5\sqrt{5}+9×\frac{\sqrt{6}}{9}-\frac{1}{2}×2\sqrt{6}+5$
$=5\sqrt{5}+\sqrt{6}-\sqrt{6}+5=5\sqrt{5}+5$。
查看更多完整答案,请扫码查看


