《2025年课堂点睛五年级数学上册人教版湖北专版》

1. 下列说法正确的是(D)。
A.因为 $2 + 2 = 2×2$,所以 $x^{2}= 2x$
B.方程 $5x = 0$ 没有解
C.$2x + 1.6＞3$ 是方程
D.方程一定是等式

答案： D

2. 当 $x = 3$,$y = 2$ 时,$x^{2}+3y= $(A)
A.15
B.12
C.9
D.8

答案： A

3. 聪聪和奇奇分别组队踢足球,聪聪队一共得了 9 分,赢了 2 场,赢一场得 3 分,平一场得 1 分,输一场不得分,____？解：设所求未知数为 $x$,则 $x + 3×2 = 9$,横线处的问题是(B)。
A.一共踢了几场比赛
B.平了多少场
C.输了多少场
D.无正确答案

答案： B

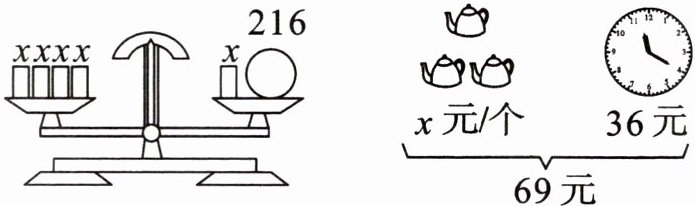
二 看图列方程,并解方程。

答案： 1. 对于天平图：
解：
根据天平平衡原理，左边$4$个$x$的重量等于右边$x + 216$的重量，可列方程$4x=x + 216$。
移项：$4x−x=x + 216−x$（等式两边同时减去$x$），得到$3x=216$。
求解：$x=\frac{216}{3}$（等式两边同时除以$3$），即$x = 72$。
2. 对于价格图：
解：
已知一个茶壶$x$元，三个茶壶和一个$36$元的物品总价为$69$元，可列方程$3x+36 = 69$。
移项：$3x+36−36 = 69−36$（等式两边同时减去$36$），得到$3x=33$。
求解：$x=\frac{33}{3}$（等式两边同时除以$3$），即$x = 11$。
综上，天平图方程的解为$x = 72$，价格图方程的解为$x = 11$。

三 学校运动场一周长 $400m$,明明和聪聪同时从同一地点同方向出发,明明每分钟跑 $250m$,聪聪每分钟跑 $300m$,至少经过多少分钟,聪聪从明明的身后追上他？

答案： 解:设聪聪x分钟后从明明的身后追上他。
(300-250)x=400
x=8
答:聪聪8分钟后从明明的身后追上他。

四 (情境题)赛龙舟是端午节最重要的节日民俗之一。甲、乙两支龙舟队同时从起点出发,向终点前进,15 秒后甲龙舟队落后乙龙舟队 $19.5m$。乙龙舟队的速度是甲龙舟队的 $2.3$ 倍,甲,乙两支龙舟队的速度分别是多少？

答案： 解:设甲龙舟队的速度是每秒xm,则乙龙舟队的速度是每秒2.3xm。
(2.3x-x)×15=19.5
x=1
2.3x=2.3×1=2.3
答:甲龙舟队的速度是1m/s,乙龙舟队的速度是2.3m/s。

五 一辆时速是 50 千米的汽车,需要多少时间才能追上 2 小时前开出的一辆时速为 40 千米的汽车？

答案： 解:设需要x小时才能追上。
40x+40×2=50x
x=8
答:需要8小时才能追上。

六 两架飞机同时从 $A$ 地飞往 $B$ 地,甲飞机每小时飞行 $300km$,乙飞机每小时飞行 $400km$。已知甲飞机比乙飞机晚到 1 小时,则 $A$、$B$ 两地的距离是多少千米？

答案： 解:设乙飞机经过x小时到达,则甲飞机经过(x+1)小时到达。
300(x+1)=400x
x=3
400x=400×3=1200
若:A,B两地的距离是1200千米。