《2025年南通小题课时作业本五年级数学上册苏教版》

【反馈练习 4】求下面组合图形的面积。（单位：厘米）

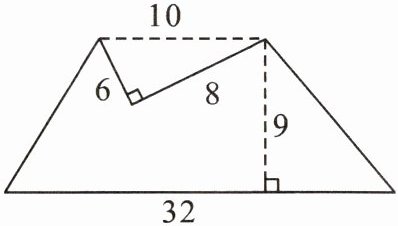
答案： 【反馈练习4】 (10+32)×9÷2-6×8÷2=165(平方厘米)

【例 5】一块三角形地的面积是 54 平方米，高是 9 米，这块地的底长为多少米？
【分析】本题是三角形面积公式的逆运用，已知三角形的面积和高，求三角形的底。
根据三角形面积公式：三角形面积=底×高÷2，求底应先用三角形面积×2÷高。

答案： 答题卡：
根据三角形面积公式：$面积 = \frac{底 × 高}{2}$。
变形得：$底 = \frac{2 × 面积}{高}$。
代入已知数值：
$底 = \frac{2 × 54}{9} = 12 (米)$。
答：三角形地的底长是$12$米。

【例 6】28 个小学生手拉手围成一个正方形，面积大约是 100 平方米。至少需要多少个这样的小学生围成面积大约是 1 公顷的大正方形？
【分析】100 平方米的正方形，边长是 10 米，28 人分成 4 份，每边是 7 人。1 公顷的大正方形的边长是 100 米，那么每边需要 10×7=70（人），4 条边一共需要 70×4=280（人）。

答案： 答题卡：
【解答】
解：$28 ÷ 4 = 7$（人）；
$1$公顷$ = 10000$平方米，正方形边长为$\sqrt{10000} = 100$（米）；
已知$100$平方米正方形边长为$10$米，每边站$7$人；
$100÷10 = 10$，则$100$米边长每边人数为$7×10 = 70$（人）；
四条边总人数为$70×4 = 280$（人）；
答：至少需要$280$个这样的小学生围成面积大约是$1$公顷的大正方形。

【例 7】一个三角形和一个平行四边形的面积相等，底也相等。如果三角形的高是 8 厘米，那么平行四边形的高是(4)厘米；如果平行四边形的高是 8 厘米，那么三角形的高是(16)厘米。
【分析】根据三角形和平行四边形面积计算公式，三角形面积是底乘高再除以 2，而平行四边形面积是底乘高，所以当三角形和平行四边形面积相等，底也相等时，三角形的高应是平行四边形高的 2 倍，平行四边形的高是三角形高的一半。

答案： 1. 4；2. 16

【例 8】（无锡实小期末）一个梯形纸片，下底是 30 厘米，上底是 20 厘米，高是 16 厘米。从梯形中剪出一个最大的三角形，剩下纸的面积是多少平方厘米？
【分析】根据题意，从梯形中剪下一个三角形，求剩余面积，用梯形面积减去三角形面积即可求出结果，梯形的上底、下底和高的数据都已给出。从梯形中剪出的最大的三角形，底是梯形最长的底，也就是 30 厘米，高与梯形的高相同。

答案： 梯形面积：$(20 + 30)×16÷2 = 50×16÷2 = 400$（平方厘米）
最大三角形面积：$30×16÷2 = 240$（平方厘米）
剩下纸的面积：$400 - 240 = 160$（平方厘米）
答：剩下纸的面积是 160 平方厘米。