《2025年新课程学习与评价五年级数学上册北师大版》

有一个自然数，除以10余7，除以7余4，除以4余1。这个自然数最小是多少？

答案： 137(一个自然数除以10余7,可以看作缺3,除以7余4,除以4余1,都可以看作缺3。如果这个自然数补上3,就能同时被10,7,4整除了,所以此题先求出10,7和4的最小公倍数,再减去3即可)

1. 写出下列分数的分母的最小公分母。
(1) $\dfrac{2}{3}$和$\dfrac{1}{6}$(6)
(2) $\dfrac{9}{10}$和$\dfrac{5}{12}$(60)
(3) $\dfrac{2}{7}$和$\dfrac{3}{8}$(56)
(4) $\dfrac{3}{4}$和$\dfrac{5}{7}$(28)
(5) $\dfrac{8}{51}$和$\dfrac{4}{17}$(51)
(6) $\dfrac{5}{22}$和$\dfrac{8}{55}$(110)

答案： 1.
(1)6
(2)60
(3)56
(4)28
(5)51
(6)110

2. 先通分，再比较大小。
(1) $\dfrac{5}{12}$和$\dfrac{7}{8}$ (2) $\dfrac{3}{10}$和$\dfrac{2}{3}$

答案： 2.
(1)$\frac{5}{12}=\frac{5×2}{12×2}=\frac{10}{24}$
(2)$\frac{3}{10}=\frac{3×3}{10×3}=\frac{9}{30}$
$\frac{7}{8}=\frac{7×3}{8×3}=\frac{21}{24}$ $\frac{2}{3}=\frac{2×10}{3×10}=\frac{20}{30}$
$\frac{5}{12}＜\frac{7}{8}$ $\frac{3}{10}＜\frac{2}{3}$

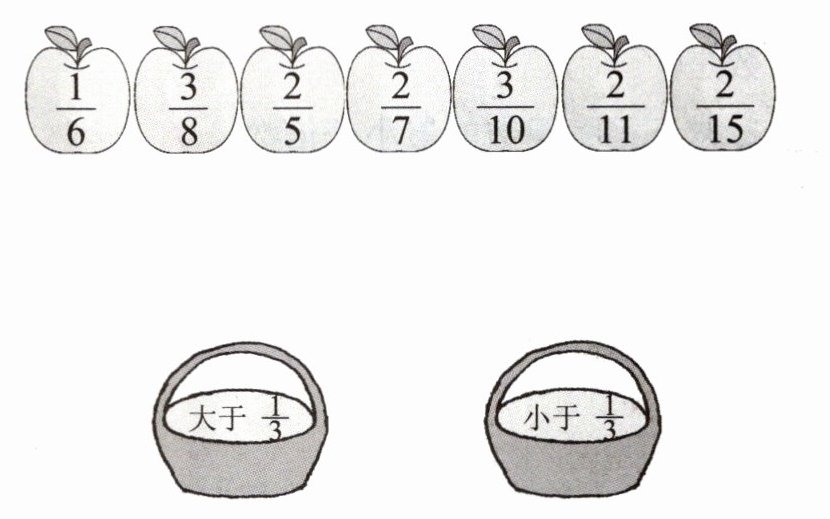
3. 连一连。

答案：
3. $\frac{1}{6}$ $\frac{3}{8}$ $\frac{2}{5}$ $\frac{2}{7}$ $\frac{3}{10}$ $\frac{2}{11}$ $\frac{2}{15}$

大于$\frac{1}{3}$ 小于$\frac{1}{3}$

4. 判断。(对的画“√”，错的画“×”)
(1) 通分和约分的依据

都

是分数的基本性质。(√)
(2) 把两个分母不相同的分数通分后，每个分数都比原来大。(×)
(3) 两个不同的合数的最小公倍数一定不等于这两个数的乘积。(×)
(4) 分母不相同的分数通分后，就变成了分数单位相同的分数。(√)
(5) 分子和分母都不相同的两个分数不能比较大小。(×)

答案： 4.
(1)√
(2)×
(3)×
(4)√
(5)×