第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
探究活动一:
1. 列式计算。
一套校服 75 元,2 套校服多少钱?
2. 分别计算长方形①,②,③的面积。
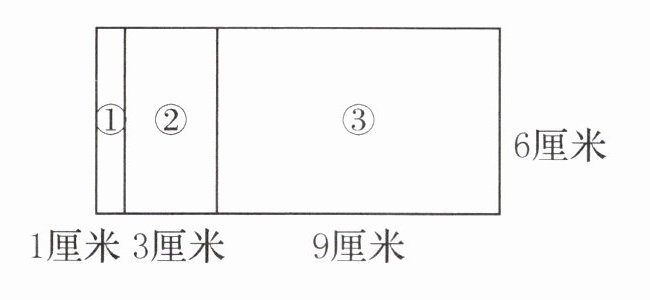
3. 观察上面两组算式,提出猜想。
一个因数不变,另一个因数( ),积( )。
4. 举例验证猜想。

用一句话总结你所发现的规律:______。
1. 列式计算。
一套校服 75 元,2 套校服多少钱?
2. 分别计算长方形①,②,③的面积。

3. 观察上面两组算式,提出猜想。
一个因数不变,另一个因数( ),积( )。
4. 举例验证猜想。

用一句话总结你所发现的规律:______。
答案:
1. 75×2=150(元),75×4=300(元),75×8=600(元)
2. ①1×6=6(平方厘米),②3×6=18(平方厘米),③9×6=54(平方厘米)
3. 乘几,也乘几
4. (1)2×5=10,2×(5×3)=30(箭头处填“×3”“×3”)
(2)4×6=24,(4×2)×6=48(箭头处填“×2”“×2”)
用一句话总结规律:一个因数不变,另一个因数乘几,积也乘几。
2. ①1×6=6(平方厘米),②3×6=18(平方厘米),③9×6=54(平方厘米)
3. 乘几,也乘几
4. (1)2×5=10,2×(5×3)=30(箭头处填“×3”“×3”)
(2)4×6=24,(4×2)×6=48(箭头处填“×2”“×2”)
用一句话总结规律:一个因数不变,另一个因数乘几,积也乘几。
探究活动二:
如果两个因数都变化,积会怎么变?请先提出你的猜想,再写几组算式验证。
猜想:一个因数( ),另一个因数( ),积( )。
验证:

请你想办法解释这种变化规律。
如果两个因数都变化,积会怎么变?请先提出你的猜想,再写几组算式验证。
猜想:一个因数( ),另一个因数( ),积( )。
验证:

请你想办法解释这种变化规律。
答案:
猜想:一个因数乘几,另一个因数乘几,积就乘这两个数的积。
验证:
(1)2×3=6
×2 ×3 ×6
4×9=36
(2)5×4=20
×4 ×2 ×8
20×8=160
解释:一个因数乘m,另一个因数乘n,积就乘m与n的积。
验证:
(1)2×3=6
×2 ×3 ×6
4×9=36
(2)5×4=20
×4 ×2 ×8
20×8=160
解释:一个因数乘m,另一个因数乘n,积就乘m与n的积。
查看更多完整答案,请扫码查看


