《2025年好课堂堂练六年级数学上册北师大版》

(1) 圆是一种( )图形,围成圆的( )长就是圆的周长,圆的周长和( )有关,( )大的圆,周长较长,( )小的圆,周长较短。

答案：
(1)封闭(曲线) 曲线(一周) 半径(直径) 半径(直径) 半径(直径)

(2) 实际上,圆的周长除以直径的商是一个固定的数,我们把它叫作( ),用字母( )表示,计算时通常取( )。

答案：
(2)圆周率 π 3.14

(3) 在我国,魏晋时期杰出的数学家( )采用“割圆术”得到圆周率的近似值是 3.14;我国南北朝时期著名的数学家( )算出π的值在( )和( )之间。这一成就在世界上领先了约 1000 年。

答案：
(3)刘徽 祖冲之 3.1415926 3.1415927

(4) 一块正方形铁皮,周长是 80 cm,要从中剪下一个最大的圆,这个圆的直径是( )cm。

答案：
(4)20

(1) 钟面上分针走一圈,分针的尖端走过的路程就形成了一个( )。

A.长方形
B.正方形
C.三角形
D.圆

答案：
(1)D

(2) 在同一个圆中,圆的周长大约是直径的( )倍。

A.4
B.3.14

答案：
(2)B

(3) 求车轮转动一周所行驶的路程就是求车轮的( )。

A.周长
B.直径
C.半径

答案：
(3)A

3. 淘气和笑笑同时从甲地去乙地,淘气沿着大圆弧走,笑笑沿着下面的中圆弧和小圆弧走(如图所示),如果他们行走的速度相同,那么谁能先到达乙地呢?

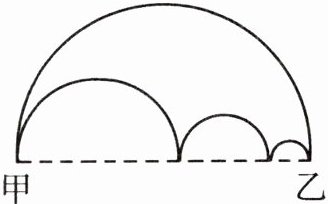
答案： 他们同时到达乙地。

4. 一棵树的树干半径是 10 厘米,爷爷想用铁丝在这棵树的树干上绕 10 圈,他现在有 6 米长的铁丝,估一估,够吗?

答案： 树干的半径是10厘米,直径则是20厘米,因为周长是直径的3倍多一些,所以周长大于60厘米,也就是说在这棵树的树干上绕10圈需要的铁丝大于6米,所以不够。

5. 如图,4 瓶横切面为圆且直径都是 7 cm 的饮料捆扎在一起,捆一圈要用的绳子长度= ( )个横切面的周长+( )条横切面直径的长度。(接头处忽略不计)

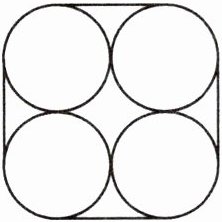
答案： 1 4