《2025年快乐练练吧同步练习六年级数学上册人教版青海专版》

1. 如图,该池塘的周长是$251.2\mathrm{m}$,池塘周围(阴影部分)是一条$5\mathrm{m}$宽的水泥路,在水泥路的外侧围一圈栏杆。水泥路的面积是多少?

答案： $251.2÷3.14÷2=40(m)$
$40+5=45(m)$
$3.14×(45^{2}-40^{2})=1334.5(m^{2})$

2. 我国古代数学名著《九章算术》方田章记载了这样一种求圆环面积的公式：“并中外周而半之,以径乘之为积步”,意思是将外圆和内圆的周长的平均数乘环的宽度可以得到环形的面积。利用这个公式求右面环形的面积,并利用我们教材上计算环形面积的方法验证结果是否正确。

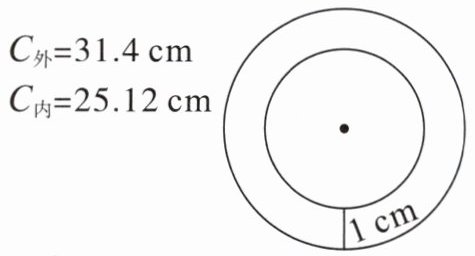
答案： $(31.4+25.12)÷2×1=28.26(cm^{2})$
$31.4÷3.14÷2=5(cm)$
$25.12÷3.14÷2=4(cm)$
$3.14×(5^{2}-4^{2})=28.26(cm^{2})$
所以结果正确。

四、培优园。
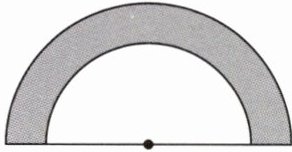
一把张开的舞蹈扇如图所示,为了装饰得更加漂亮,要在图中阴影部分加装饰布料。已知扇子的最外边沿长$15.7\mathrm{dm}$,需要装饰的部分环宽$1\mathrm{dm}$。需要准备多少装饰布料?

答案： 外环半径:$15.7÷3.14=5(dm)$
内环半径:$5-1=4(dm)$
阴影部分的面积:$[3.14×(5^{2}-4^{2})]×\frac{1}{2}=14.13(dm^{2})$