1. 下面四张扑克牌中,绕中心顺时针旋转180°后还和原来一样的是(

D
).
答案:
D
2. 如图,△ABC与△DEF关于点O成中心对称.下列结论不成立的是(
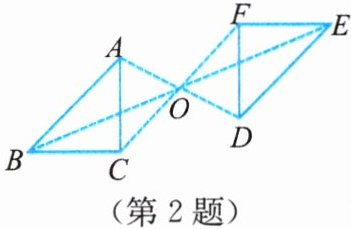
A.点A与点D是对称点
B.BO= EO
C.AB//DE
D.∠ACB= ∠FDE
D
).
A.点A与点D是对称点
B.BO= EO
C.AB//DE
D.∠ACB= ∠FDE
答案:
D
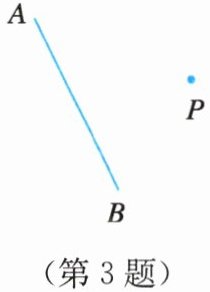
3. 如图,已知线段AB和点P,作线段CD,使CD与AB关于点P成中心对称.

答案:
【解析】:
本题考查中心对称的性质及作图方法,需要利用点$P$是中心对称点的性质,作出线段$AB$关于点$P$成中心对称的线段$CD$。
中心对称的性质为:在平面内,把一个图形绕着某个点旋转$180^{\circ }$,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
所以对于线段$AB$上的任意一点,其关于点$P$的对称点与该点到点$P$的距离相等,且在同一条直线上,只是方向相反。
作图步骤如下:
连接$AP$并延长$AP$到点$C$,使得$AP = PC$(即点$C$是点$A$关于点$P$的对称点)。
连接$BP$并延长$BP$到点$D$,使得$BP = PD$(即点$D$是点$B$关于点$P$的对称点)。
连接$CD$,则线段$CD$就是线段$AB$关于点$P$成中心对称的线段。
【答案】:
图略(按照上述步骤作出线段$CD$,使$CD$与$AB$关于点$P$成中心对称)。
本题考查中心对称的性质及作图方法,需要利用点$P$是中心对称点的性质,作出线段$AB$关于点$P$成中心对称的线段$CD$。
中心对称的性质为:在平面内,把一个图形绕着某个点旋转$180^{\circ }$,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
所以对于线段$AB$上的任意一点,其关于点$P$的对称点与该点到点$P$的距离相等,且在同一条直线上,只是方向相反。
作图步骤如下:
连接$AP$并延长$AP$到点$C$,使得$AP = PC$(即点$C$是点$A$关于点$P$的对称点)。
连接$BP$并延长$BP$到点$D$,使得$BP = PD$(即点$D$是点$B$关于点$P$的对称点)。
连接$CD$,则线段$CD$就是线段$AB$关于点$P$成中心对称的线段。
【答案】:
图略(按照上述步骤作出线段$CD$,使$CD$与$AB$关于点$P$成中心对称)。
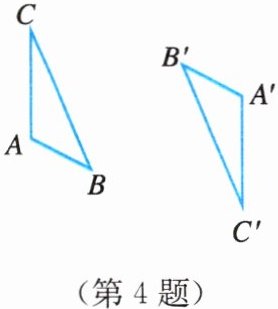
4. 如图,△ABC和△A′B′C′关于点O成中心对称,请找出它们的对称中心O.

答案:
解:连接AA',连接CC',AA'与CC'相交于点O,点O即为对称中心。
查看更多完整答案,请扫码查看


