《2025年口算训练五年级数学上册北师大版双色升级版》

1. 根据分数涂一涂,并比较大小。
=；=；=；=

答案： 解析：本题考查分数的意义以及分数大小的比较。
第一组：$\frac{1}{2}$和$\frac{4}{8}$
第一个圆被平均分成2份，涂其中1份，表示$\frac{1}{2}$；
第二个圆被平均分成8份，涂其中4份，表示$\frac{4}{8}$。
因为$\frac{1}{2}=\frac{4}{8}$，所以$\frac{1}{2}◯\frac{4}{8}$中$◯$填“$=$”。
第二组：$\frac{1}{3}$和$\frac{2}{6}$
第一个长方形被平均分成3份，涂其中1份，表示$\frac{1}{3}$；
第二个长方形被平均分成6份，涂其中2份，表示$\frac{2}{6}$。
因为$\frac{1}{3}=\frac{2}{6}$，所以$\frac{1}{3}◯\frac{2}{6}$中$◯$填“$=$”。
第三组：$\frac{6}{8}$和$\frac{3}{4}$
第一个圆被平均分成8份，涂其中6份，表示$\frac{6}{8}$；
第二个圆被平均分成4份，涂其中3份，表示$\frac{3}{4}$。
因为$\frac{6}{8}=\frac{3}{4}$，所以$\frac{6}{8}◯\frac{3}{4}$中$◯$填“$=$”。
第四组：$\frac{9}{12}$和$\frac{3}{4}$
第一个正方形被平均分成12份，涂其中9份，表示$\frac{9}{12}$；
第二个正方形被平均分成4份，涂其中3份，表示$\frac{3}{4}$。
因为$\frac{9}{12}=\frac{3}{4}$，所以$\frac{9}{12}◯\frac{3}{4}$中$◯$填“$=$”。
答案：$=$；$=$；$=$；$=$。

2. 用分数表示涂色部分,并比较大小。

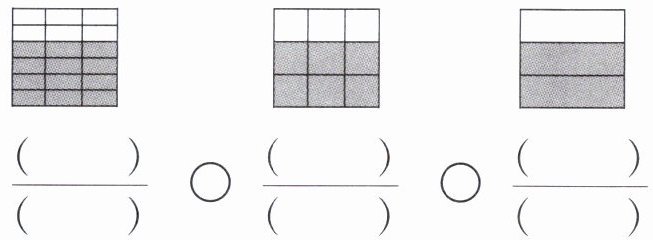
$\frac{12}{16}$$=$$\frac{6}{8}$$=$$\frac{3}{4}$

答案： $\frac{12}{16}$；$=$；$\frac{6}{8}$；$=$；$\frac{3}{4}$

在( )里填上合适的数。
$\frac {1}{3}= \frac {1×2}{3×2}= \frac {(2)}{(6)}$ $\frac {2}{5}= \frac {2×(7)}{5×(7)}= \frac {14}{35}$
$\frac {18}{24}= \frac {18÷(6)}{24÷(6)}= \frac {(3)}{4}$ $\frac {72}{27}= \frac {(72)÷(9)}{(27)÷(9)}= \frac {8}{(3)}$
$\frac {3}{8}= \frac {12}{(32)}= \frac {(18)}{48}$ $\frac {36}{60}= \frac {6}{(10)}= \frac {(3)}{5}$

答案： 解析：本题主要考察分数的性质，即分数的分子和分母同时乘以或除以同一个数（0除外），分数的大小不变。
对于 $\frac{1}{3} = \frac{1 × 2}{3 × 2} = \frac{( )}{( )}$：
分子分母同时乘以2，得到 $\frac{2}{6}$，所以填空为 $\frac{2}{6}$。
对于 $\frac{2}{5} = \frac{2 × ( )}{5 × ( )} = \frac{14}{35}$：
因为 $14 = 2 × 7$，$35 = 5 × 7$，所以填空为 $\frac{2 × 7}{5 × 7}$，即都乘以7。
对于 $\frac{18}{24} = \frac{18 ÷ ( )}{24 ÷ ( )} = \frac{( )}{4}$：
因为 $24 ÷ 6 = 4$，所以分子分母同时除以6，得到 $\frac{3}{4}$，填空为 $\frac{18 ÷ 6}{24 ÷ 6} = \frac{3}{4}$。
对于 $\frac{72}{27} = \frac{( ) ÷ ( )}{( ) ÷ ( )} = \frac{8}{( )}$：
因为 $72 ÷ 9 = 8$，$27 ÷ 9 = 3$，所以填空为 $\frac{72 ÷ 9}{27 ÷ 9} = \frac{8}{3}$。
对于 $\frac{3}{8} = \frac{12}{( )} = \frac{( )}{48}$：
因为 $12 = 3 × 4$，所以分母应为 $8 × 4 = 32$；
又因为 $48 = 8 × 6$，所以分子应为 $3 × 6 = 18$，填空为 $\frac{12}{32} = \frac{18}{48}$。
对于 $\frac{36}{60} = \frac{6}{( )} = \frac{( )}{5}$：
因为 $36 ÷ 6 = 6$，$60 ÷ 6 = 10$，所以第一个填空分母为10；
又因为 $60 ÷ 12 = 5$，所以分子应为 $36 ÷ 12 = 3$，填空为 $\frac{6}{10} = \frac{3}{5}$。
答案：
$\frac{1}{3} = \frac{1 × 2}{3 × 2} = \frac{2}{6}$，
填空为 2；6。
$\frac{2}{5} = \frac{2 × 7}{5 × 7} = \frac{14}{35}$，
填空为 7；7。
$\frac{18}{24} = \frac{18 ÷ 6}{24 ÷ 6} = \frac{3}{4}$，
填空为 6；6；3。
$\frac{72}{27} = \frac{72 ÷ 9}{27 ÷ 9} = \frac{8}{3}$，
填空为 72；9；27；9；3。
$\frac{3}{8} = \frac{12}{32} = \frac{18}{48}$，
填空为 32；18。
$\frac{36}{60} = \frac{6}{10} = \frac{3}{5}$，
填空为 10；3。

$\frac {5}{12}$的分子加上15,要使分数的大小不变,分母应加几？
秘籍点拨 分子加15,$5+15= 20$,相当于分子乘4,根据分数基本性质,分母也应乘4。

答案： 解析：
题目考查的是分数的基本性质，即分子分母同时乘或除以同一个数（0除外），分数的大小不变。
题目中给出$\frac{5}{12}$的分子加上15，变为20，这相当于分子乘4（因为$20 ÷ 5 = 4$）。
为了保持分数的大小不变，分母也应该乘4。
原来的分母是12，乘4后变为$12 × 4 = 48$。
需要找出分母应加上多少才能变为48，即$48 - 12 = 36$。
答案：
分母应加36。