2025年暑假生活海燕出版社六年级综合
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活海燕出版社六年级综合 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
(3)不改变小数的大小,把3.6改写成三位小数是(
③
)。
答案:
【解析】:
本题考察的是小数的基本性质和改写。根据小数的性质,我们知道在小数的末尾添上“0”或者去掉”0“,小数的大小不变。因此,要将3.6改写成三位小数,我们只需在3.6后面加两个0,即3.600。
【答案】:
③ 3.600
本题考察的是小数的基本性质和改写。根据小数的性质,我们知道在小数的末尾添上“0”或者去掉”0“,小数的大小不变。因此,要将3.6改写成三位小数,我们只需在3.6后面加两个0,即3.600。
【答案】:
③ 3.600
个、十、百、千、万……都是
③
。
答案:
【解析】:
本题考查的是对数学基本概念的理解。题目中列出的“个、十、百、千、万……”在数学中是用来计数的标准,即这些词汇代表的是数的不同量级,用于帮助我们理解和表达大数。我们需要从给定的选项①数位、②位数、③计数单位中,选择最符合这些词汇性质的选项。
①“数位”通常指的是数字在数中的位置,如个位、十位等,它描述的是数字的位置属性,而不是用来计数的单位。
②“位数”则是指一个数由多少个数字组成,如123是一个三位数,它描述的是数的组成复杂度,同样不是用来计数的单位。
③“计数单位”则是用来计量数的标准单位,如个、十、百、千、万等,它们直接对应着数的不同量级,是用来计数和表示数的大小的基本单位。
因此,根据这些词汇的性质和用途,我们可以确定它们都是“计数单位”。
【答案】:
③ 计数单位。
本题考查的是对数学基本概念的理解。题目中列出的“个、十、百、千、万……”在数学中是用来计数的标准,即这些词汇代表的是数的不同量级,用于帮助我们理解和表达大数。我们需要从给定的选项①数位、②位数、③计数单位中,选择最符合这些词汇性质的选项。
①“数位”通常指的是数字在数中的位置,如个位、十位等,它描述的是数字的位置属性,而不是用来计数的单位。
②“位数”则是指一个数由多少个数字组成,如123是一个三位数,它描述的是数的组成复杂度,同样不是用来计数的单位。
③“计数单位”则是用来计量数的标准单位,如个、十、百、千、万等,它们直接对应着数的不同量级,是用来计数和表示数的大小的基本单位。
因此,根据这些词汇的性质和用途,我们可以确定它们都是“计数单位”。
【答案】:
③ 计数单位。
(5)要使四位数425□是3的倍数,□里最小应填(
③
)。
答案:
【解析】:
本题考查的是3的倍数的特征。
一个数如果是3的倍数,那么它的各位数字之和也一定是3的倍数。
要找出使四位数425□成为3的倍数的最小数字,可以先计算已知的三位数字之和,即4+2+5=11。
接下来,尝试将0-9这10个数字分别加到11上,看哪个结果能被3整除,并且是最小的那个。
尝试数字0,得到11+0=11,不是3的倍数;
尝试数字1,得到11+1=12,是3的倍数,并且是目前尝试中的最小值。
因此,可以确定□里最小应填的数字是1。
【答案】:③。
本题考查的是3的倍数的特征。
一个数如果是3的倍数,那么它的各位数字之和也一定是3的倍数。
要找出使四位数425□成为3的倍数的最小数字,可以先计算已知的三位数字之和,即4+2+5=11。
接下来,尝试将0-9这10个数字分别加到11上,看哪个结果能被3整除,并且是最小的那个。
尝试数字0,得到11+0=11,不是3的倍数;
尝试数字1,得到11+1=12,是3的倍数,并且是目前尝试中的最小值。
因此,可以确定□里最小应填的数字是1。
【答案】:③。
(6)两个大于1的自然数的积一定是(
③
)。
答案:
【解析】:
这个问题涉及到自然数、偶数、质数、合数的定义及它们的性质。首先,我们要明确这几个数学术语的定义,然后根据这些定义去分析两个大于1的自然数的积的性质。
1. 自然数:用以计量事物的件数或表示事物次序的数,即用数码0,1,2,3,4……所表示的数。
2. 偶数:能够被2整除的整数。
3. 质数:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数。
4. 合数:一个大于1的自然数,除了1和它本身以外还有其他的因数,这样的数就叫合数。
接下来,我们分析两个大于1的自然数的积:
对于选项①(偶数):两个大于1的自然数的积不一定是偶数。例如,1.5×2=3,3是奇数。但是,如果两个数中至少有一个是偶数,那么它们的积一定是偶数。由于题目没有限定两个数的奇偶性,所以我们不能确定它们的积一定是偶数。
对于选项②(质数):质数是只有两个正因数(1和本身)的自然数。两个大于1的自然数的积至少有三个因数(1,两个数本身,以及它们的积),所以它们的积不可能是质数。
对于选项③(合数):由于两个大于1的自然数的积至少有三个因数(1,两个乘数,积本身),这符合合数的定义。因此,我们可以确定它们的积一定是合数。
【答案】:
③ 合数
这个问题涉及到自然数、偶数、质数、合数的定义及它们的性质。首先,我们要明确这几个数学术语的定义,然后根据这些定义去分析两个大于1的自然数的积的性质。
1. 自然数:用以计量事物的件数或表示事物次序的数,即用数码0,1,2,3,4……所表示的数。
2. 偶数:能够被2整除的整数。
3. 质数:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数。
4. 合数:一个大于1的自然数,除了1和它本身以外还有其他的因数,这样的数就叫合数。
接下来,我们分析两个大于1的自然数的积:
对于选项①(偶数):两个大于1的自然数的积不一定是偶数。例如,1.5×2=3,3是奇数。但是,如果两个数中至少有一个是偶数,那么它们的积一定是偶数。由于题目没有限定两个数的奇偶性,所以我们不能确定它们的积一定是偶数。
对于选项②(质数):质数是只有两个正因数(1和本身)的自然数。两个大于1的自然数的积至少有三个因数(1,两个数本身,以及它们的积),所以它们的积不可能是质数。
对于选项③(合数):由于两个大于1的自然数的积至少有三个因数(1,两个乘数,积本身),这符合合数的定义。因此,我们可以确定它们的积一定是合数。
【答案】:
③ 合数
4. 小明从家到学校需要走25分钟,早上7:35从家出发,什么时间可以到达学校?
答案:
【解析】:本题主要考察时间的加法运算。小明从家到学校走路需要25分钟,已知出发时间为早上7:35,我们需要将这个时间加上走路所需的时间来得到到达学校的时间。
【答案】:
出发时间是7:35,走路所需时间是25分钟。
所以,到达学校的时间 = 出发时间 + 走路所需时间
= 7:35 + 25分钟
= 8:00。
所以,小明早上7:35从家出发,可以在8:00到达学校。
【答案】:
出发时间是7:35,走路所需时间是25分钟。
所以,到达学校的时间 = 出发时间 + 走路所需时间
= 7:35 + 25分钟
= 8:00。
所以,小明早上7:35从家出发,可以在8:00到达学校。
5. 2019年9月8日,中华人民共和国第十一届少数民族传统体育运动会在郑州举行。这个月共有多少天?有哪几个月与这个月的天数相同?这一年是不是闰年?共有多少天?
答案:
【解析】:
本题主要考查了月份天数的知识、闰年的判定以及一年中天数的计算。
首先,需要知道9月有多少天,根据常识,9月是个小月,有30天。
接着,需要找出哪些月份与9月的天数相同,根据月份天数的知识,可以知道4月、6月、11月也是小月,各有30天。
最后,需要判断2019年是否为闰年,并计算这一年的天数。根据闰年的定义,能被4整除但不能被100整除的年份,或者能被400整除的年份是闰年。2019年不能被4整除,所以不是闰年,是平年,平年有365天。
【答案】:
这个月共有30天。
有4月、6月、11月与这个月的天数相同。
这一年不是闰年,是平年,共有365天。
本题主要考查了月份天数的知识、闰年的判定以及一年中天数的计算。
首先,需要知道9月有多少天,根据常识,9月是个小月,有30天。
接着,需要找出哪些月份与9月的天数相同,根据月份天数的知识,可以知道4月、6月、11月也是小月,各有30天。
最后,需要判断2019年是否为闰年,并计算这一年的天数。根据闰年的定义,能被4整除但不能被100整除的年份,或者能被400整除的年份是闰年。2019年不能被4整除,所以不是闰年,是平年,平年有365天。
【答案】:
这个月共有30天。
有4月、6月、11月与这个月的天数相同。
这一年不是闰年,是平年,共有365天。
6. 小丽家每周大约用水1500升,她家每年大约用多少升水?
答案:
【解析】:本题主要考察乘法运算及年份中周数的常识。
为了计算小丽家每年大约用多少升水,我们需要知道一年有多少周,然后将每周的用水量乘以周数。
通常,一年有52周(不考虑闰年中的额外一天对周数的影响,因为这对整体结果影响很小)。
所以,我们可以通过将每周用水量1500升乘以52周来得到每年的用水量。
【答案】:
解:
$每年用水量 = 每周用水量 × 每年周数$
$每年用水量 = 1500 升/周 × 52 周 = 78000 升$
答:小丽家每年大约用78000升水。
为了计算小丽家每年大约用多少升水,我们需要知道一年有多少周,然后将每周的用水量乘以周数。
通常,一年有52周(不考虑闰年中的额外一天对周数的影响,因为这对整体结果影响很小)。
所以,我们可以通过将每周用水量1500升乘以52周来得到每年的用水量。
【答案】:
解:
$每年用水量 = 每周用水量 × 每年周数$
$每年用水量 = 1500 升/周 × 52 周 = 78000 升$
答:小丽家每年大约用78000升水。
下面是2020年7月的月历,小强做了一个空心“ ”框,用它可以套住月历中的5个数(如图)。
”框,用它可以套住月历中的5个数(如图)。
(1)这5个数的平均数是多少?
(2)如果套住的5个数中,最中间的那个数是11,这5个数的和是多少?
(3)如果套住的5个数的和是85,请用空心“ ”把这5个数框起来。
”把这5个数框起来。
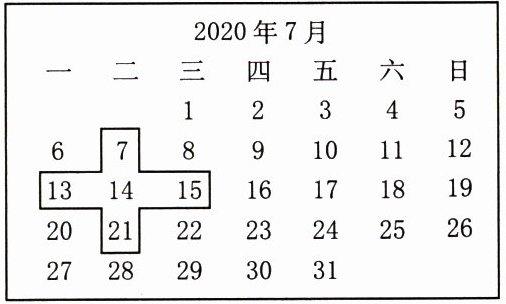
 ”框,用它可以套住月历中的5个数(如图)。
”框,用它可以套住月历中的5个数(如图)。(1)这5个数的平均数是多少?
(2)如果套住的5个数中,最中间的那个数是11,这5个数的和是多少?
(3)如果套住的5个数的和是85,请用空心“
 ”把这5个数框起来。
”把这5个数框起来。
答案:
(1)设中间数为$x$,则其余四个数分别为$x - 7$、$x + 7$、$x - 1$、$x + 1$。这5个数的和为$(x - 7)+(x + 7)+(x - 1)+(x + 1)+x = 5x$,平均数为$5x÷5 = x$。
(2)中间数是11,和是$5×11 = 55$。
(3)设中间数为$x$,$5x = 85$,$x = 17$。这5个数是10、17、24、16、18。在月历中框出10(五)、16(四)、17(五)、18(六)、24(五)。
(1)设中间数为$x$,则其余四个数分别为$x - 7$、$x + 7$、$x - 1$、$x + 1$。这5个数的和为$(x - 7)+(x + 7)+(x - 1)+(x + 1)+x = 5x$,平均数为$5x÷5 = x$。
(2)中间数是11,和是$5×11 = 55$。
(3)设中间数为$x$,$5x = 85$,$x = 17$。这5个数是10、17、24、16、18。在月历中框出10(五)、16(四)、17(五)、18(六)、24(五)。
查看更多完整答案,请扫码查看


