第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
11. 如图所示,电源电压为 $ 3 V $,$ R_0 $ 的阻值为 $ 5 \Omega $,滑动变阻器 $ R $ 的最大阻值为 $ 10 \Omega $,$ a $、$ b $ 为滑动变阻器两个端点。闭合开关,下列说法正确的是(

A.若将滑片移动到 $ a $ 端,电路仍能正常工作
B.滑片在 $ b $ 端时,电流表 $ A_1 $ 示数为 $ 0.3 A $
C.滑片由 $ b $ 端向 $ a $ 端移动,电流表 $ A_2 $ 示数变大
D.滑片移动到中点时,电流表 $ A_1 $ 与 $ A_2 $ 示数比为 $ 2 : 1 $
D
)
A.若将滑片移动到 $ a $ 端,电路仍能正常工作
B.滑片在 $ b $ 端时,电流表 $ A_1 $ 示数为 $ 0.3 A $
C.滑片由 $ b $ 端向 $ a $ 端移动,电流表 $ A_2 $ 示数变大
D.滑片移动到中点时,电流表 $ A_1 $ 与 $ A_2 $ 示数比为 $ 2 : 1 $
答案:
D
12. 如图所示,滑动变阻器 $ R_2 $ 的最大阻值与定值电阻 $ R_1 $ 相等。闭合开关 $ S $,当滑片 $ P $ 在 $ a $ 端时,电压表示数为 $ 2 V $,则电源电压为
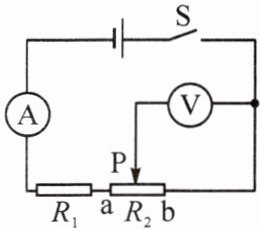
4
$ V $,此时电流表示数为 $ I_1 $,当滑片 $ P $ 向右滑动时,电压表示数变小
(填“变大”“变小”或“不变”),当滑片 $ P $ 在 $ b $ 端时,电流表示数为 $ I_2 $,则 $ I_1 : I_2 = $1:1
。
答案:
4 变小 1:1
13. 在图甲所示的电路中,电源电压保持不变,滑动变阻器 $ R_2 $ 上标有“$ 20 \Omega $ $ 2 A $”字样,闭合开关后,当滑动变阻器的滑片 $ P $ 在中点位置时,电流表 $ A_1 $、$ A $ 的示数分别如图乙、丙所示,求:
(1)电源电压。
(2)电阻 $ R_1 $ 的阻值。
(3)改变滑片 $ P $ 的位置,使电流表 $ A $ 与电压表 $ V $ 的指针偏离零刻度线的角度(即偏离的格数)恰好相同,求此时滑动变阻器 $ R_2 $ 接入电路的阻值。
(4)滑动变阻器 $ R_2 $ 工作时的最小电流。
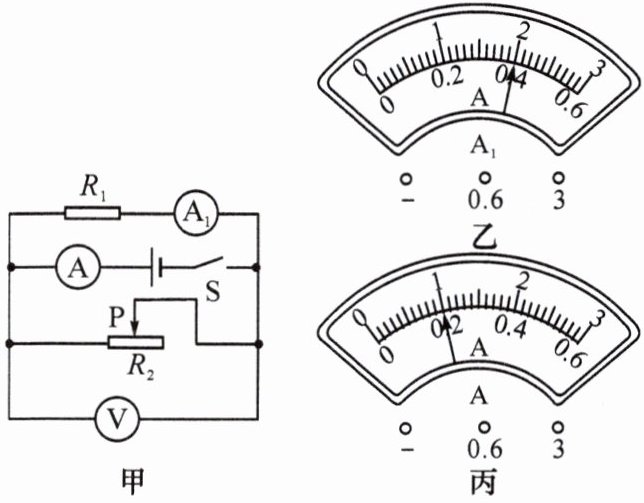
(1)电源电压。
(2)电阻 $ R_1 $ 的阻值。
(3)改变滑片 $ P $ 的位置,使电流表 $ A $ 与电压表 $ V $ 的指针偏离零刻度线的角度(即偏离的格数)恰好相同,求此时滑动变阻器 $ R_2 $ 接入电路的阻值。
(4)滑动变阻器 $ R_2 $ 工作时的最小电流。

答案:
解:
(1)电流表A处于干路,$A_{1}$处于支路,且电流表$A_{1}$指针的偏角大于电流表A指针的偏角,所以电流表$A_{1}$的测量范围为0~0.6A,通过$R_{1}$的电流$I_{1}=0.4A$
电流表A的测量范围为0~3A,干路电流$I=1A$则通过滑动变阻器的电流:
$I_{2}=I-I_{1}=1A-0.4A=0.6A$
电源电压:$U=I_{2}×\frac {1}{2}R_{2}=0.6A×\frac {1}{2}×20\Omega =6V$
(2)$R_{1}$的阻值:$R_{1}=\frac {U}{I_{1}}=\frac {6V}{0.4A}=15\Omega $
(3)因电源电压6V保持不变,所以滑片移动时,电压表的示数为6V不变,对应的测量范围为0~15V,分度值为0.5V,偏离的格数:
$n=\frac {6V}{0.5V}=12$
电流表A的示数:$I'=12×0.1A=1.2A$
此时通过滑动变阻器的电流:$I_{2}'=I'-I_{1}=1.2A-0.4A=0.8A$
滑动变阻器接入电路中的阻值:
$R_{2}'=\frac {U}{I_{2}'}=\frac {6V}{0.8A}=7.5\Omega $
(4)当变阻器连入电路中的阻值最大时,工作电流最小:
$I_{2min}=\frac {U}{R_{2}}=\frac {6V}{20\Omega }=0.3A$
(1)电流表A处于干路,$A_{1}$处于支路,且电流表$A_{1}$指针的偏角大于电流表A指针的偏角,所以电流表$A_{1}$的测量范围为0~0.6A,通过$R_{1}$的电流$I_{1}=0.4A$
电流表A的测量范围为0~3A,干路电流$I=1A$则通过滑动变阻器的电流:
$I_{2}=I-I_{1}=1A-0.4A=0.6A$
电源电压:$U=I_{2}×\frac {1}{2}R_{2}=0.6A×\frac {1}{2}×20\Omega =6V$
(2)$R_{1}$的阻值:$R_{1}=\frac {U}{I_{1}}=\frac {6V}{0.4A}=15\Omega $
(3)因电源电压6V保持不变,所以滑片移动时,电压表的示数为6V不变,对应的测量范围为0~15V,分度值为0.5V,偏离的格数:
$n=\frac {6V}{0.5V}=12$
电流表A的示数:$I'=12×0.1A=1.2A$
此时通过滑动变阻器的电流:$I_{2}'=I'-I_{1}=1.2A-0.4A=0.8A$
滑动变阻器接入电路中的阻值:
$R_{2}'=\frac {U}{I_{2}'}=\frac {6V}{0.8A}=7.5\Omega $
(4)当变阻器连入电路中的阻值最大时,工作电流最小:
$I_{2min}=\frac {U}{R_{2}}=\frac {6V}{20\Omega }=0.3A$
查看更多完整答案,请扫码查看


