《2025年启东中学作业本八年级数学上册人教版》

5. 如图,在四边形 ABDC 中,$AC = AB$,$DC = DB$,$∠BAC = 60^{\circ}$,$∠CDB = 120^{\circ}$,E 是 AC 上一点,F 是 AB 的延长线上一点,且$CE = BF$,连接 AD,DF,DE。
(1) 求证：①$DE = DF$；②$∠ADB = 60^{\circ}$。
(2) 若点 G 在 AB 上,且$∠EDG = 60^{\circ}$,连接 EG,猜想 CE,EG,BG 之间的数量关系,并说明理由。

答案：
(1)①在四边形ABDC中,∠BAC=60°,∠CDB=120°.
∵∠BAC+∠ABD+∠CDB+∠C=360°,
∴∠ABD+∠C=180°,
又
∵∠ABD+∠DBF=180°,
∴∠C=∠DBF.
在△CDE和△BDF中,CE=BF,∠C=∠DBF,DC=DB,
∴△CDE≌△BDF(SAS).
∴DE=DF.
②在△ACD和△ABD中,AC=AB,DC=DB,AD=AD,
∴△ACD≌△ABD(SSS),
∴∠ADC=∠ADB.
又
∵∠CDB=120°,
∴∠ADB=60°.
(2)解:EG=GB+CE.理由如下:
∵∠CDB=120°,∠EDG=60°,
∴∠CDE+∠BDG=60°.
由
(1)知△CDE≌△BDF,
∴∠CDE=∠FDB.
∴∠GDF=∠BDG+∠BDF=∠CDE+∠BDG=60°,
又
∵∠EDG=60°,
∴∠EDG=∠GDF.
在△EDG和△FDG中,DE=DF,∠EDG=∠GDF,
DG=DG,
∴△EDG≌△FDG(SAS).
∴EG=GF=GB+BF=GB+CE.

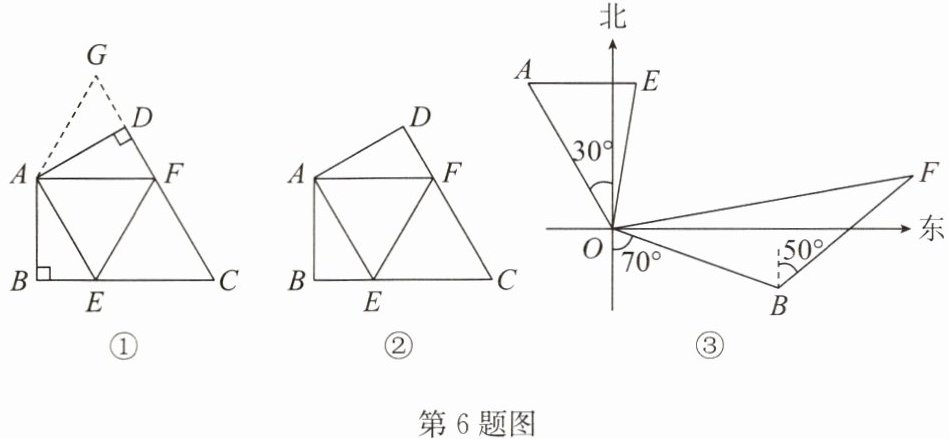
6. 【问题提出】在一次课上,老师出了这样一道题：如图①,在四边形 ABCD 中,$AB = AD$,$∠BAD = 120^{\circ}$,$∠B = ∠ADC = 90^{\circ}$,E,F 分别是 BC,CD 上的点,且$∠EAF = 60^{\circ}$,试探究图①中线段 BE,EF,FD 之间的数量关系. 小亮同学认为：延长 FD 到点 G,使$DG = BE$,连接 AG,先证明$△ABE\cong △ADG$,再证明$△AEF\cong △AGF$,则可得到 BE,EF,FD 之间的数量关系是______。
【探索延伸】如图②,在四边形 ABCD 中,$AB = AD$,$∠B + ∠D = 180^{\circ}$,E,F 分别是 BC,CD 上的点,$∠EAF = \frac {1}{2}∠BAD$,上述结论是否仍然成立？请说明理由。
【结论运用】如图③,台风中心位于小岛(O 处)北偏西$30^{\circ}$的 A 处,台风中心风力 12 级,每远离台风中心 40 千米,风力就会减弱一级. 某货轮位于小岛南偏东$70^{\circ}$的 B 处,并且台风中心和货轮到小岛的距离相等,如果台风中心向正东方向以 40 海里/时的速度前进,同时该货轮沿北偏东$50^{\circ}$方向以 60 海里/时的速度前进,2 小时后,它们分别到达 E,F 处,且$∠EOF = 70^{\circ}$,问此时该货轮受到台风影响的最大风力有几级？(1 海里$= 1.852$千米)

答案：
【问题提出】EF=BE+FD
【探索延伸】解:结论仍然成立.
理由:如答图①,延长FD到点G,使DG=BE,连接AG.
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG.
在△ABE和△ADG中,AB=AD,
∠B=∠ADG,
BE=DG,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∴∠BAE+∠EAD=∠DAG+∠EAD,
∴∠BAD=∠EAG.
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,AE=AG,
∠EAF=∠GAF,
AF=AF,
∴△AEF≌△AGF(SAS),
∴EF=FG=DG+FD=BE+DF.

【结论运用】解:如答图②,延长AE,BF,交于点C,连接EF.
∵∠AOB=30°+90°+(90° - 70°)=140°,∠EOF=70°,
∴∠EOF=$\frac{1}{2}$∠AOB.
∵OA=OB,
∠OAC+∠OBC=(90° - 30°)+(70°+50°)=180°,
∴符合【探索延伸】中的条件,
∴EF=AE+BF仍然成立.
EF=2×40+2×60=200(海里),
200×1.852=370.4(千米),
∴此时该货轮受到台风影响的最大风力级数为12 - $\frac{370.4}{40}$=2.74(级).
答:此时该货轮受到台风影响的最大风力有2.74级.