2025年暑假课程练习南方出版社六年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假课程练习南方出版社六年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
一、判断。(对的画“√”,错的画“×”)
1. 如果一个圆锥的底面半径扩大到原来的2倍,高缩小到原来的$\frac {1}{4}$,那么体积不变。(
2. 如果两个圆柱体的侧面积相等,它们的底面周长一定相等。(
3. 用智能切割技术将一段圆柱形钢材精准截成相同的两段,体积不变,但表面积会增加。(
4. 为了节约材料,工厂将一段圆柱形环保钢材加工成体积最大的圆锥零件,削去部分的体积是原钢材体积的$\frac {1}{3}$。(
1. 如果一个圆锥的底面半径扩大到原来的2倍,高缩小到原来的$\frac {1}{4}$,那么体积不变。(
√
)2. 如果两个圆柱体的侧面积相等,它们的底面周长一定相等。(
×
)3. 用智能切割技术将一段圆柱形钢材精准截成相同的两段,体积不变,但表面积会增加。(
√
)4. 为了节约材料,工厂将一段圆柱形环保钢材加工成体积最大的圆锥零件,削去部分的体积是原钢材体积的$\frac {1}{3}$。(
×
)
答案:
1.√ 2.× 3.√ 4.×
1. 某现代建筑中的圆柱形立柱,侧面展开后是正方形,其底面直径与高的比是(
A. $1:π$
B. $π:1$
C. $1:2π$
A
)。A. $1:π$
B. $π:1$
C. $1:2π$
答案:
1.A
2. 若一个圆锥的底面半径扩大为原来的2倍,高扩大为原来的3倍,则它的体积(
A. 扩大为原来的4倍
B. 扩大为原来的6倍
C. 扩大为原来的12倍
C
)。A. 扩大为原来的4倍
B. 扩大为原来的6倍
C. 扩大为原来的12倍
答案:
2.C
3. 一个圆柱体侧面展开后是正方形,这个圆柱体的底面直径与高的比是(
A. $1:π$
B. $π:1$
C. $1:2π$
A
)。A. $1:π$
B. $π:1$
C. $1:2π$
答案:
3.A
三、填表。
| |半径|直径|高|表面积|体积|
|--|--|--|--|--|--|
|圆柱|5 cm| |2 cm| | |
| | |6 dm|4 dm| | |
| |6 cm| |3 cm| | |
|圆锥| |8 cm|9 cm| | |
| |10 dm| |6 dm| | |
| | |4 m|15 m| | |
| |半径|直径|高|表面积|体积|
|--|--|--|--|--|--|
|圆柱|5 cm| |2 cm| | |
| | |6 dm|4 dm| | |
| |6 cm| |3 cm| | |
|圆锥| |8 cm|9 cm| | |
| |10 dm| |6 dm| | |
| | |4 m|15 m| | |
答案:
【解析】:
1. 对于第一个圆柱:已知半径$r = 5$cm,根据$d = 2r$,可得直径$d=2\times5 = 10$cm;圆柱表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times5^{2}+2\times3.14\times5\times2=157 + 62.8 = 219.8$ $cm^{2}$;体积$V=\pi r^{2}h=3.14\times5^{2}\times2 = 157$ $cm^{3}$。
2. 对于第二个圆柱:已知直径$d = 6$dm,则半径$r=\frac{d}{2}=\frac{6}{2}=3$dm;表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times3^{2}+2\times3.14\times3\times4=56.52+75.36 = 131.88$ $dm^{2}$;体积$V=\pi r^{2}h=3.14\times3^{2}\times4 = 113.04$ $dm^{3}$。
3. 对于第三个圆柱:已知直径$d = 6$cm,则半径$r=\frac{d}{2}=\frac{6}{2}=3$cm;表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times3^{2}+2\times3.14\times3\times3=56.52 + 56.52=113.04$ $cm^{2}$;体积$V=\pi r^{2}h=3.14\times3^{2}\times3 = 84.78$ $cm^{3}$。
4. 对于第一个圆锥:已知直径$d = 8$cm,则半径$r=\frac{d}{2}=\frac{8}{2}=4$cm;圆锥表面积$S=\pi rl+\pi r^{2}$($l$为母线长,$l=\sqrt{r^{2}+h^{2}}=\sqrt{4^{2}+9^{2}}=\sqrt{16 + 81}=\sqrt{97}\approx9.85$),这里一般小学阶段不要求求圆锥表面积,只考虑体积,体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times4^{2}\times9 = 150.72$ $cm^{3}$。
5. 对于第二个圆锥:已知直径$d = 10$dm,则半径$r=\frac{d}{2}=\frac{10}{2}=5$dm;体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times5^{2}\times6 = 157$ $dm^{3}$。
6. 对于第三个圆锥:已知直径$d = 4$m,则半径$r=\frac{d}{2}=\frac{4}{2}=2$m;体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times2^{2}\times15 = 62.8$ $m^{3}$。
【答案】:
1. 10 cm;219.8 $cm^{2}$;157 $cm^{3}$
2. 3 dm;131.88 $dm^{2}$;113.04 $dm^{3}$
3. 3 cm;113.04 $cm^{2}$;84.78 $cm^{3}$
4. 4 cm;150.72 $cm^{3}$
5. 5 dm;157 $dm^{3}$
6. 2 m;62.8 $m^{3}$
1. 对于第一个圆柱:已知半径$r = 5$cm,根据$d = 2r$,可得直径$d=2\times5 = 10$cm;圆柱表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times5^{2}+2\times3.14\times5\times2=157 + 62.8 = 219.8$ $cm^{2}$;体积$V=\pi r^{2}h=3.14\times5^{2}\times2 = 157$ $cm^{3}$。
2. 对于第二个圆柱:已知直径$d = 6$dm,则半径$r=\frac{d}{2}=\frac{6}{2}=3$dm;表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times3^{2}+2\times3.14\times3\times4=56.52+75.36 = 131.88$ $dm^{2}$;体积$V=\pi r^{2}h=3.14\times3^{2}\times4 = 113.04$ $dm^{3}$。
3. 对于第三个圆柱:已知直径$d = 6$cm,则半径$r=\frac{d}{2}=\frac{6}{2}=3$cm;表面积$S = 2\pi r^{2}+2\pi rh=2\times3.14\times3^{2}+2\times3.14\times3\times3=56.52 + 56.52=113.04$ $cm^{2}$;体积$V=\pi r^{2}h=3.14\times3^{2}\times3 = 84.78$ $cm^{3}$。
4. 对于第一个圆锥:已知直径$d = 8$cm,则半径$r=\frac{d}{2}=\frac{8}{2}=4$cm;圆锥表面积$S=\pi rl+\pi r^{2}$($l$为母线长,$l=\sqrt{r^{2}+h^{2}}=\sqrt{4^{2}+9^{2}}=\sqrt{16 + 81}=\sqrt{97}\approx9.85$),这里一般小学阶段不要求求圆锥表面积,只考虑体积,体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times4^{2}\times9 = 150.72$ $cm^{3}$。
5. 对于第二个圆锥:已知直径$d = 10$dm,则半径$r=\frac{d}{2}=\frac{10}{2}=5$dm;体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times5^{2}\times6 = 157$ $dm^{3}$。
6. 对于第三个圆锥:已知直径$d = 4$m,则半径$r=\frac{d}{2}=\frac{4}{2}=2$m;体积$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\times3.14\times2^{2}\times15 = 62.8$ $m^{3}$。
【答案】:
1. 10 cm;219.8 $cm^{2}$;157 $cm^{3}$
2. 3 dm;131.88 $dm^{2}$;113.04 $dm^{3}$
3. 3 cm;113.04 $cm^{2}$;84.78 $cm^{3}$
4. 4 cm;150.72 $cm^{3}$
5. 5 dm;157 $dm^{3}$
6. 2 m;62.8 $m^{3}$
四、动手操作。
1. 用这张纸可以做(
2. 圆柱的底面半径是(
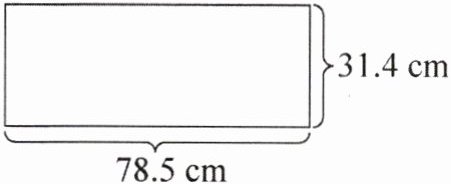
1. 用这张纸可以做(
2
)个不同的圆柱。2. 圆柱的底面半径是(
12.5
)cm或(5
)cm。
答案:
1.2 2.12.5 5(或“5 12.5”)
查看更多完整答案,请扫码查看


