2025年暑假课程练习南方出版社六年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假课程练习南方出版社六年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 过一点可以画(
无数
)条射线,过两点可以画(一
)条线段。
答案:
1. 无数 2. 一
2. 线段有(
2
)个端点,射线有(1
)个端点,直线(没有
)端点。
答案:
2 1 没有
3. 两条直线相交,组成四个角,如果其中一个角是$90^{\circ }$,那么其他三个角都是(
$90^{\circ}$
),这两条直线叫做(互相垂直
)。
答案:
$90^{\circ}$;互相垂直
4. 在6点钟时,时针与分针组成(
平
)角;9点钟时,时针与分针组成(直
)角。
答案:
平 直
5. 一个等腰三角形的底角是$45^{\circ }$,它的顶角是(
90
)度,它是一个(直角
)三角形。
答案:
90,直角
6. 等边三角形有(
3
)条对称轴,长方形有(2
)条对称轴,圆有(无数
)条对称轴。
答案:
3 2 无数
二、判断。(对的画“√”,错的画“×”)
1. 在同一平面内,两条永不相交的直线,叫做平行线。 (
2. 过一点可以画无数条直线。(
3. 大于$90^{\circ }$的角都是钝角。 (
4. 圆心决定圆的位置,半径决定圆的大小。 (
5. 因为射线和直线都无法测量长度,所以它们无法比较长短。(
6. 平行四边形一定是轴对称图形。 (
1. 在同一平面内,两条永不相交的直线,叫做平行线。 (
√
)2. 过一点可以画无数条直线。(
√
)3. 大于$90^{\circ }$的角都是钝角。 (
×
)4. 圆心决定圆的位置,半径决定圆的大小。 (
√
)5. 因为射线和直线都无法测量长度,所以它们无法比较长短。(
√
)6. 平行四边形一定是轴对称图形。 (
×
)
答案:
1.√ 2.√ 3.× 4.√ 5.√ 6.×
1. 一个三角形中,其中一个角是$100^{\circ }$,这个三角形是(
A. 锐角
B. 钝角
C. 直角
B
)三角形。A. 锐角
B. 钝角
C. 直角
答案:
B
2. 钟面上分针走一圈,时针转动的角度是(
A. $90^{\circ }$
B. $60^{\circ }$
C. $30^{\circ }$
C
)。A. $90^{\circ }$
B. $60^{\circ }$
C. $30^{\circ }$
答案:
C
3. 过直线外一点作已知直线的平行线,可作(
A. 1
B. 2
C. 无数
A
)条。A. 1
B. 2
C. 无数
答案:
A
四、实践操作。
过P点作射线OA的平行线,作射线OB的垂线。
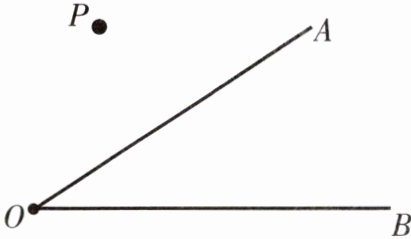
过P点作射线OA的平行线,作射线OB的垂线。

按照以下方法作图:1. 作射线OA的平行线:把三角板的一条直角边与OA重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板原来和OA重合的直角边经过点P,过点P沿三角板的这条直角边画直线。2. 作射线OB的垂线:把三角板的一条直角边与OB重合,沿射线OB移动三角板,使三角板的另一条直角边经过点P,过点P沿三角板的这条直角边画直线。
答案:
【解析】:
1. 作射线$OA$的平行线:
把三角板的一条直角边与$OA$重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板原来和$OA$重合的直角边经过点$P$,过点$P$沿三角板的这条直角边画直线,这条直线就是与$OA$平行的直线。
2. 作射线$OB$的垂线:
把三角板的一条直角边与$OB$重合,沿射线$OB$移动三角板,使三角板的另一条直角边经过点$P$,过点$P$沿三角板的这条直角边画直线,这条直线就是$OB$的垂线。
【答案】:按照上述方法作出图形(由于是操作题,无法用文字精确表述最终图形,需根据上述方法实际作图)。
1. 作射线$OA$的平行线:
把三角板的一条直角边与$OA$重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板原来和$OA$重合的直角边经过点$P$,过点$P$沿三角板的这条直角边画直线,这条直线就是与$OA$平行的直线。
2. 作射线$OB$的垂线:
把三角板的一条直角边与$OB$重合,沿射线$OB$移动三角板,使三角板的另一条直角边经过点$P$,过点$P$沿三角板的这条直角边画直线,这条直线就是$OB$的垂线。
【答案】:按照上述方法作出图形(由于是操作题,无法用文字精确表述最终图形,需根据上述方法实际作图)。
五、解决问题。
下图是一个直角三角形,求出∠1和∠2的度数。
∠1=
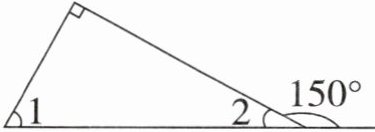
下图是一个直角三角形,求出∠1和∠2的度数。
∠1=
60°
,∠2=30°

答案:
60° 30°
查看更多完整答案,请扫码查看


