第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
数一数,图中共有多少个三角形?

思路导引:如图,把大三角形分成两类,分别数出每类三角形的个数,再求和即可。
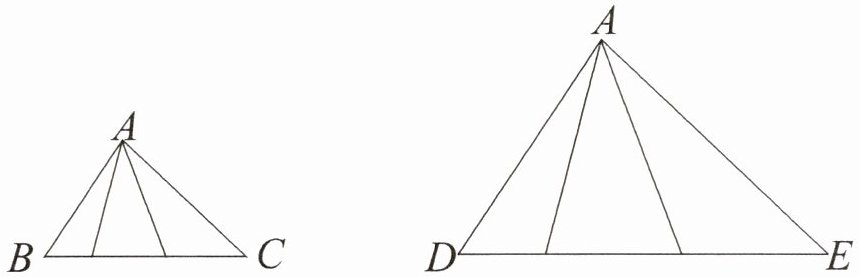
观察这两幅图,发现BC边和DE边上的每条线段都能与顶点A构成一个三角形,也就是说,BC边和DE边上有多少条线段,图中就有多少个三角形。
BC边上有$3+2+1= 6$(条)线段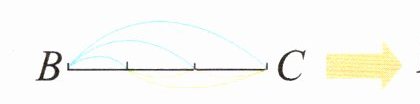
同理可得,DE边上也有$3+2+1= 6$(条)线段。所以图中共有$6×2= 12$(个)三角形。

思路导引:如图,把大三角形分成两类,分别数出每类三角形的个数,再求和即可。

观察这两幅图,发现BC边和DE边上的每条线段都能与顶点A构成一个三角形,也就是说,BC边和DE边上有多少条线段,图中就有多少个三角形。
BC边上有$3+2+1= 6$(条)线段

同理可得,DE边上也有$3+2+1= 6$(条)线段。所以图中共有$6×2= 12$(个)三角形。
答案:
规范解答:$(3+2+1)×2= 12$(个)
答:图中共有12个三角形。
答:图中共有12个三角形。
1. 数一数,下面各图中分别有多少个三角形?


答案:
1.
(1)$(4+3+2+1)×2=20$(个)
答:图中有 20 个三角形。
(2)$(3+2+1)×3=18$(个)
答:图中有 18 个三角形。
(1)$(4+3+2+1)×2=20$(个)
答:图中有 20 个三角形。
(2)$(3+2+1)×3=18$(个)
答:图中有 18 个三角形。
查看更多完整答案,请扫码查看


