《2025年一本暑假衔接四升五数学人教版浙江专版》

4.(山东·济南)按要求完成下面各题。
(1)在研究四边形的内角和时,有四位同学表达了他们的想法,填一填。

(2)你最喜欢()的方法,请你用这种方法探究五边形的内角和,先在图中画一画,再算一算。

答案：

(1)$180^{\circ }×3-180^{\circ }=360^{\circ }$
$180^{\circ }×4-360^{\circ }=360^{\circ }$
(2)答案不唯一，示例:
乐乐

$180^{\circ }×3=540^{\circ }$

5. 李伯伯家的菜地是一个直角三角形,其中较大的锐角的度数是较小的锐角的2倍。这两个锐角分别是多少度?

答案： 较小的锐角：$90^{\circ }÷(2+1)=30^{\circ }$
较大的锐角：$30^{\circ }×2=60^{\circ }$
答:这两个锐角分别是$30^{\circ }$、$60^{\circ }$。

6. 乐乐用一根铁丝编了一个等腰三角形,测量得到这个等腰三角形中一个内角的度数是$64^{\circ }$,这个等腰三角形的其他两个内角分别是多少度?

答案： 顶角是$64^{\circ }$时:$(180^{\circ }-64^{\circ })÷2=58^{\circ }$
底角是$64^{\circ }$时:$180^{\circ }-64^{\circ }×2=52^{\circ }$
答:这个等腰三角形的其他两个内角分别是$58^{\circ }$、$58^{\circ }$或$64^{\circ }$、$52^{\circ }$。

7. 将一张长方形纸按照如图所示的方式折叠,已知$∠1= ∠2$,则$∠3$是多少度?

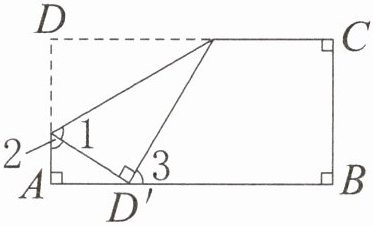
答案： $∠1=∠2=180^{\circ }÷3=60^{\circ }$
$∠3=180^{\circ }-(180^{\circ }-60^{\circ }-90^{\circ }+90^{\circ })=60^{\circ }$
答:$∠3$是$60^{\circ }$。