1. 已知$\odot O$的半径为8cm,圆心O到直线l的距离为9cm,则直线l与$\odot O$的公共点的个数为 (
A. 0
B. 1
C. 2
D. 无法确定
A
)A. 0
B. 1
C. 2
D. 无法确定
答案:
A
2. (2023眉山)如图5-M-1,AB切$\odot O$于点B,连接OA交$\odot O$于点C,$BD// OA交\odot O$于点D,连接CD,若$∠OCD= 25^{\circ }$,则$∠A$的度数为 (
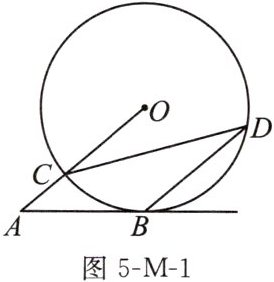
A. $25^{\circ }$
B. $35^{\circ }$
C. $40^{\circ }$
D. $45^{\circ }$
C
)
A. $25^{\circ }$
B. $35^{\circ }$
C. $40^{\circ }$
D. $45^{\circ }$
答案:
C
3. 如图5-M-2,以点P为圆心作圆,所得的圆与直线l相切的是 (
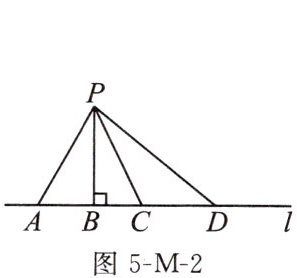
A. 以PA的长为半径的圆
B. 以PB的长为半径的圆
C. 以PC的长为半径的圆
D. 以PD的长为半径的圆
B
)
A. 以PA的长为半径的圆
B. 以PB的长为半径的圆
C. 以PC的长为半径的圆
D. 以PD的长为半径的圆
答案:
B
4. 如图5-M-3,五边形ABCDE是$\odot O$的内接正五边形,则正五边形中心角$∠COD$的度数是 (
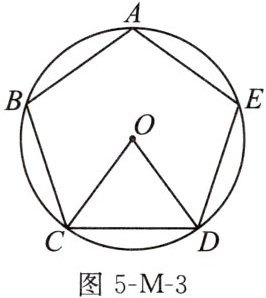
A. $60^{\circ }$
B. $36^{\circ }$
C. $76^{\circ }$
D. $72^{\circ }$
D
)
A. $60^{\circ }$
B. $36^{\circ }$
C. $76^{\circ }$
D. $72^{\circ }$
答案:
D
5. 如图5-M-4,PA,PB切$\odot O$于点A,B,MN切$\odot O$于点C,交PB于点N,交PA于点M.若$PA= 7.5cm$,则$\triangle PMN$的周长是 (

A. 7.5 cm
B. 10 cm
C. 15 cm
D. 12.5 cm
C
)
A. 7.5 cm
B. 10 cm
C. 15 cm
D. 12.5 cm
答案:
C
6. (2023江阴月考)若点$B(a,0)$在以点$A(1,0)$为圆心,2为半径的圆内,则a的取值范围为 (
A. $a<-1$
B. $a>3$
C. $-1<a<3$
D. $a≥-1且a≠0$
C
)A. $a<-1$
B. $a>3$
C. $-1<a<3$
D. $a≥-1且a≠0$
答案:
C
7. 如图5-M-5,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直,垂足为M.若$∠ABC= 55^{\circ }$,则$∠ACD$的度数为 (
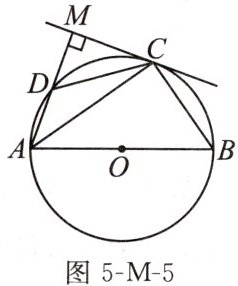
A. $20^{\circ }$
B. $35^{\circ }$
C. $40^{\circ }$
D. $55^{\circ }$
A
)
A. $20^{\circ }$
B. $35^{\circ }$
C. $40^{\circ }$
D. $55^{\circ }$
答案:
A
8. 如图5-M-6,$\odot O是\triangle ABC$的内切圆,$∠ACB= 90^{\circ },AB= 8,∠BOC= 105^{\circ }$,则BC的长为 (
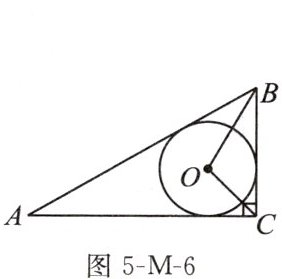
A. 4
B. 3
C. 5
D. $4\sqrt {3}$
A
)
A. 4
B. 3
C. 5
D. $4\sqrt {3}$
答案:
A
9. 如图5-M-7,AB是$\odot O$的直径,点C在AB的延长线上,CD与$\odot O$相切于点D,若$∠A= 40^{\circ }$,则$∠C= $______$^{\circ }$.
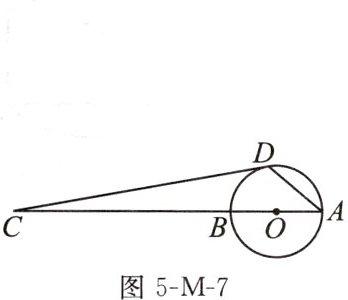

答案:
10
10. 如图5-M-8,正五边形ABCDE内接于$\odot O$,连接AC,则$∠BAC$的度数是______

$36^{\circ}$
.
答案:
$36 ^ { \circ }$
11. 如图5-M-9,将$\triangle ABC$绕点C顺时针旋转$120^{\circ }得到\triangle A'B'C$,已知$AC= 3,BC= 2$,则线段AB扫过的图形(阴影部分)的面积为
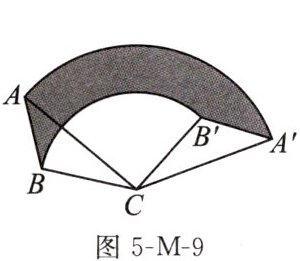
$\frac { 5 } { 3 } \pi$
.
答案:
$ \frac { 5 } { 3 } \pi $
12. 已知圆锥的母线长为4,底面圆的半径为3,该圆锥的侧面展开图的面积为
12π
.
答案:
$ 12 \pi $
13. (2023青岛)如图5-M-10,在平面直角坐标系中,已知点$A(1,0),P(-1,0),\odot P$过原点O,且与x轴交于另一点D,AB为$\odot P$的切线,B为切点,BC是$\odot P$的直径,则$∠BCD$的度数为______
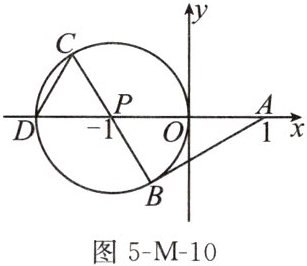
$60^{\circ}$
.
答案:
$ 60 ^ { \circ } $
查看更多完整答案,请扫码查看


