14. 如图5-M-11,已知$\odot O内切于Rt\triangle ABC,∠C= 90^{\circ }$,BC边上的切点为D.作$\odot O$的直径DE,连接AE并延长交BC于点F,若$∠AFC= 45^{\circ },FD= 2$,则AB的长为______
5
.
答案:
5
15. (18分)如图5-M-12,正方形ABCD内接于$\odot O$,P为$\overset{\frown }{BC}$上的一点(点P不与点B,C重合),连接DP,CP.
(1)求$∠CPD$的度数为
(2)若$\odot O$的半径为r,则阴影部分的面积是______
(3)当P为$\overset{\frown }{BC}$的中点时,CP是$\odot O$的内接正n边形的一边,求n的值为
(1)求$∠CPD$的度数为
$45^{\circ}$
;(2)若$\odot O$的半径为r,则阴影部分的面积是______
$\frac{\pi r^{2}}{4}-\frac{1}{2}r^{2}$
;(3)当P为$\overset{\frown }{BC}$的中点时,CP是$\odot O$的内接正n边形的一边,求n的值为
8
.
答案:
1. (1)
解:连接$OC$,$OD$。
因为正方形$ABCD$内接于$\odot O$,所以$\angle DOC = 90^{\circ}$。
根据圆周角定理:同弧所对的圆周角是圆心角的一半,$\angle CPD=\frac{1}{2}\angle DOC$。
所以$\angle CPD = 45^{\circ}$。
2. (2)
解:阴影部分的面积$S = S_{扇形DOC}-S_{\triangle DOC}$。
已知$\odot O$半径为$r$,$S_{扇形DOC}=\frac{90\pi r^{2}}{360}=\frac{\pi r^{2}}{4}$,$S_{\triangle DOC}=\frac{1}{2}r\cdot r=\frac{1}{2}r^{2}$。
所以$S=\frac{\pi r^{2}}{4}-\frac{1}{2}r^{2}$。
3. (3)
解:连接$OP$。
因为$P$为$\overset{\frown }{BC}$的中点,$\angle BOC = 90^{\circ}$,所以$\angle COP=\frac{1}{2}\angle BOC = 45^{\circ}$。
又因为正$n$边形的中心角$\alpha=\frac{360^{\circ}}{n}$,这里$\alpha = 45^{\circ}$。
由$\frac{360^{\circ}}{n}=45^{\circ}$,解得$n = 8$。
综上,答案依次为:(1)$45^{\circ}$;(2)$\frac{\pi r^{2}}{4}-\frac{1}{2}r^{2}$;(3)$8$。
解:连接$OC$,$OD$。
因为正方形$ABCD$内接于$\odot O$,所以$\angle DOC = 90^{\circ}$。
根据圆周角定理:同弧所对的圆周角是圆心角的一半,$\angle CPD=\frac{1}{2}\angle DOC$。
所以$\angle CPD = 45^{\circ}$。
2. (2)
解:阴影部分的面积$S = S_{扇形DOC}-S_{\triangle DOC}$。
已知$\odot O$半径为$r$,$S_{扇形DOC}=\frac{90\pi r^{2}}{360}=\frac{\pi r^{2}}{4}$,$S_{\triangle DOC}=\frac{1}{2}r\cdot r=\frac{1}{2}r^{2}$。
所以$S=\frac{\pi r^{2}}{4}-\frac{1}{2}r^{2}$。
3. (3)
解:连接$OP$。
因为$P$为$\overset{\frown }{BC}$的中点,$\angle BOC = 90^{\circ}$,所以$\angle COP=\frac{1}{2}\angle BOC = 45^{\circ}$。
又因为正$n$边形的中心角$\alpha=\frac{360^{\circ}}{n}$,这里$\alpha = 45^{\circ}$。
由$\frac{360^{\circ}}{n}=45^{\circ}$,解得$n = 8$。
综上,答案依次为:(1)$45^{\circ}$;(2)$\frac{\pi r^{2}}{4}-\frac{1}{2}r^{2}$;(3)$8$。
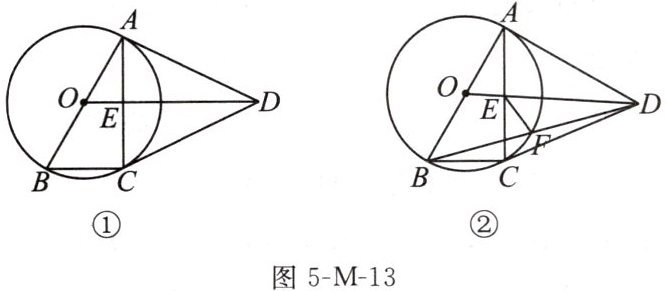
16. (20分)如图5-M-13,在四边形ABCD中,$AB= AD= CD$,以AB为直径的$\odot O$经过点C,连接AC,OD交于点E.
(1)如图①,求证:$OD// BC;$
(2)如图②,若AD是$\odot O$的切线,连接BD交$\odot O$于点F,连接EF.若$OA= \sqrt {5}$,求EF的长.
(1)如图①,求证:$OD// BC;$
(2)如图②,若AD是$\odot O$的切线,连接BD交$\odot O$于点F,连接EF.若$OA= \sqrt {5}$,求EF的长.

答案:
解:
(1)证明:如图①,连接 $ OC $.
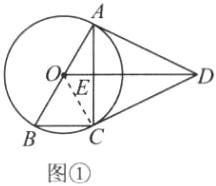
则 $ O A = O C $.
又 $ \because A D = C D $,$ \therefore O D $ 垂直平分 $ A C $.
$ \therefore \angle D E C = 90 ^ { \circ } $.
$ \because A B $ 为 $ \odot O $ 的直径,
$ \therefore \angle A C B = 90 ^ { \circ } $.
$ \therefore \angle A C B = \angle D E C $.$ \therefore O D // B C $.
(2)如图②,连接 $ A F $,过点 $ F $ 作 $ F M \perp E F $ 交 $ O D $ 于点 $ M $.
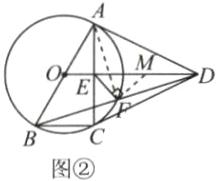
$ \because O D // B C $,$ \therefore \angle M D F = \angle F B C $.
$ \because \widehat { F C } = \widehat { F C } $,
$ \therefore \angle F B C = \angle F A E $,
$ \therefore \angle F A E = \angle M D F $.
$ \because A B = A D $,$ A B $ 为 $ \odot O $ 的直径,$ A D $ 是 $ \odot O $ 的切线,
$ \therefore \angle A F B = 90 ^ { \circ } $,$ \triangle A B D $ 为等腰直角三角形.
$ \therefore \angle D A F = 45 ^ { \circ } $.
$ \because \angle A F D = 90 ^ { \circ } $,
$ \therefore \angle D A F = \angle A D F = 45 ^ { \circ } $.
$ \therefore A F = D F $.
$ \because \angle E F M = \angle A F D = 90 ^ { \circ } $,
$ \therefore \angle A F E = \angle D F M $.
$ \therefore \triangle A E F \cong \triangle D M F ( A S A ) $.
$ \therefore A E = D M $,$ E F = M F $.
$ \because O A = \sqrt { 5 } $,$ \therefore A B = A D = 2 \sqrt { 5 } $.
$ \therefore O D = \sqrt { O A ^ { 2 } + A D ^ { 2 } } = 5 $.
又 $ \because \angle A E D = 90 ^ { \circ } $,
$ \therefore A E = D M = \frac { \sqrt { 5 } \times 2 \sqrt { 5 } } { 5 } = 2 $.
$ \therefore D E = \sqrt { A D ^ { 2 } - A E ^ { 2 } } = 4 $.
$ \therefore E M = D E - D M = 4 - 2 = 2 $.
则易得 $ E F = \sqrt { 2 } $.
解:
(1)证明:如图①,连接 $ OC $.

则 $ O A = O C $.
又 $ \because A D = C D $,$ \therefore O D $ 垂直平分 $ A C $.
$ \therefore \angle D E C = 90 ^ { \circ } $.
$ \because A B $ 为 $ \odot O $ 的直径,
$ \therefore \angle A C B = 90 ^ { \circ } $.
$ \therefore \angle A C B = \angle D E C $.$ \therefore O D // B C $.
(2)如图②,连接 $ A F $,过点 $ F $ 作 $ F M \perp E F $ 交 $ O D $ 于点 $ M $.

$ \because O D // B C $,$ \therefore \angle M D F = \angle F B C $.
$ \because \widehat { F C } = \widehat { F C } $,
$ \therefore \angle F B C = \angle F A E $,
$ \therefore \angle F A E = \angle M D F $.
$ \because A B = A D $,$ A B $ 为 $ \odot O $ 的直径,$ A D $ 是 $ \odot O $ 的切线,
$ \therefore \angle A F B = 90 ^ { \circ } $,$ \triangle A B D $ 为等腰直角三角形.
$ \therefore \angle D A F = 45 ^ { \circ } $.
$ \because \angle A F D = 90 ^ { \circ } $,
$ \therefore \angle D A F = \angle A D F = 45 ^ { \circ } $.
$ \therefore A F = D F $.
$ \because \angle E F M = \angle A F D = 90 ^ { \circ } $,
$ \therefore \angle A F E = \angle D F M $.
$ \therefore \triangle A E F \cong \triangle D M F ( A S A ) $.
$ \therefore A E = D M $,$ E F = M F $.
$ \because O A = \sqrt { 5 } $,$ \therefore A B = A D = 2 \sqrt { 5 } $.
$ \therefore O D = \sqrt { O A ^ { 2 } + A D ^ { 2 } } = 5 $.
又 $ \because \angle A E D = 90 ^ { \circ } $,
$ \therefore A E = D M = \frac { \sqrt { 5 } \times 2 \sqrt { 5 } } { 5 } = 2 $.
$ \therefore D E = \sqrt { A D ^ { 2 } - A E ^ { 2 } } = 4 $.
$ \therefore E M = D E - D M = 4 - 2 = 2 $.
则易得 $ E F = \sqrt { 2 } $.
查看更多完整答案,请扫码查看


