《2025年全品学练考九年级数学上册苏科版江苏专版》

14. (14分)如图6-M-10,AB是$\odot O$的直径,四边形ABCD内接于$\odot O$,D是$\overset{\frown}{AC}$的中点,$DE\perp BC$交BC的延长线于点E,连接BD.
(1)求证:DE是$\odot O$的切线;
(2)若$AB= 10$,$BC= 8$,求EC的长.

答案： 1. （1）**证明$DE$是$\odot O$的切线**：
连接$OD$。
因为$D$是$\overset{\frown}{AC}$的中点，所以$\overset{\frown}{AD}=\overset{\frown}{CD}$，根据圆心角、弧、弦的关系定理，可得$\angle ABD=\angle CBD$。
又因为$OB = OD$，所以$\angle ODB=\angle ABD$（等边对等角）。
那么$\angle ODB=\angle CBD$，所以$OD// BE$（内错角相等，两直线平行）。
已知$DE\perp BC$，即$\angle E = 90^{\circ}$，因为$OD// BE$，所以$\angle ODE+\angle E=180^{\circ}$（两直线平行，同旁内角互补）。
则$\angle ODE = 90^{\circ}$，即$OD\perp DE$。
又因为$OD$是$\odot O$的半径，所以$DE$是$\odot O$的切线。
2. （2）**求$EC$的长**：
连接$AC$。
因为$AB$是$\odot O$的直径，所以$\angle ACB = 90^{\circ}$（直径所对的圆周角是直角）。
在$Rt\triangle ABC$中，$AB = 10$，$BC = 8$，根据勾股定理$a^{2}+b^{2}=c^{2}$（这里$c = AB$，$a = BC$，$b = AC$），可得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-8^{2}}=\sqrt{100 - 64}=\sqrt{36}=6$。
由（1）知$\angle ODE=\angle E=\angle ACB = 90^{\circ}$，且$OD// BE$，$OA = OB$，设$OD$交$AC$于点$F$，则$AF = CF=\frac{1}{2}AC = 3$，$OF=\frac{1}{2}BC = 4$（三角形中位线定理：三角形的中位线平行于第三边且等于第三边的一半），所以$OD=\frac{1}{2}AB = 5$，则$DF=OD - OF=5 - 4 = 1$。
因为$\angle E=\angle ACB$，$\angle DCE+\angle BCD = 180^{\circ}$，$\angle BAD+\angle BCD = 180^{\circ}$（圆内接四边形的对角互补），所以$\angle DCE=\angle BAD$，又$\angle BAD=\angle BDC$（同弧所对的圆周角相等），所以$\angle DCE=\angle BDC$。
又$\angle E=\angle ACB = 90^{\circ}$，所以四边形$FDEC$是矩形（有三个角是直角的四边形是矩形），则$EC = DF$。
所以$EC = 1$。
综上，（1）证明见上述过程；（2）$EC$的长为$1$。

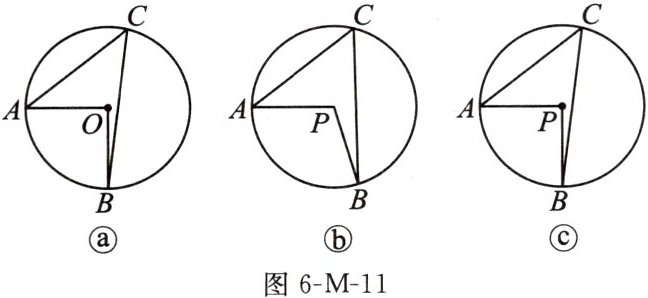
15. (15分)如图6-M-11,已知A,B为圆上两定点,点C在该圆上,$\angle C为\overset{\frown}{AB}$所对的圆周角.
知识回顾
(1)如图ⓐ,$\odot O$中,点B,C位于直线AO异侧,$\angle AOB+\angle C= 135^{\circ}$.
①求$\angle C$的度数;
②若$\odot O$的半径为5,$AC= 8$,求BC的长.
逆向思考
(2)如图ⓑ,若P为圆内一点,且$\angle APB＜120^{\circ}$,$PA= PB$,$\angle APB= 2\angle C$.求证:P为该圆的圆心.
拓展应用
(3)如图ⓒ,在(2)的条件下,若$\angle APB= 90^{\circ}$,点C在$\odot P$位于直线AP上方部分的圆弧上运动,点D在$\odot P$上.求证:满足$CD= \sqrt{2}CB-CA$的所有点D中,必有一个点的位置始终不变.

答案：
解:
(1)①$\because \angle A O B + \angle C = 135 ^ { \circ } , \angle A O B = 2 \angle C$,
$\therefore 3 \angle C = 135 ^ { \circ } , \therefore \angle C = 45 ^ { \circ }$.
②连接AB,过点A作$ A M \perp B C $,垂足为M,如图(a).

$\because \angle C = 45 ^ { \circ } , A C = 8 , \therefore \triangle A C M $是等腰直角三角形,且易得$ A M = C M = 4 \sqrt { 2 } $.
$\because \angle A O B = 2 \angle C = 90 ^ { \circ } , O A = O B $,
$\therefore \triangle A O B $是等腰直角三角形,
$\therefore $易得$ A B = \sqrt { 2 } O A = 5 \sqrt { 2 } $.
在$ \mathrm { Rt } \triangle A B M $中,$ B M = \sqrt { A B ^ { 2 } - A M ^ { 2 } } = 3 \sqrt { 2 } $,
$\therefore B C = C M + B M = 4 \sqrt { 2 } + 3 \sqrt { 2 } = 7 \sqrt { 2 } $.
(2)证明:延长AP交圆于点N,连接BN,如图(b),则$ \angle C = \angle N $.

$\because \angle A P B = 2 \angle C $,
$\therefore \angle A P B = 2 \angle N $.
$\because \angle A P B = \angle N + \angle P B N $,
$\therefore \angle N = \angle P B N $,
$\therefore P N = P B $.
$\because P A = P B , \therefore P A = P B = P N $,
$\therefore P $为该圆的圆心.
(3)证明:过点B作BC的垂线交CA的延长线于点E,连接AB,延长AP交$ \odot P $于点F,连接CF,FB,如图(c).

$\because \angle A P B = 90 ^ { \circ } $,
$\therefore \angle A C B = 45 ^ { \circ } $,
$\therefore \triangle B C E $是等腰直角三角形,
$\therefore B E = B C $.
易得$ E C = \sqrt { 2 } C B $.
$\because B P \perp A F , P A = P F $,
$\therefore B A = B F $.
$\because A F $是$ \odot P $的直径,
$\therefore \angle A B F = 90 ^ { \circ } $,
$\therefore \angle E B C = \angle A B F = 90 ^ { \circ } $,
$\therefore \angle E B A = \angle C B F $,
$\therefore \triangle E B A \cong \triangle C B F ( \mathrm { SAS } ) $,
$\therefore A E = C F $.
$\because C D = \sqrt { 2 } C B - C A = C E - C A = A E $,
$\therefore C D = C F $,
$\therefore $必有一个点D的位置始终不变,即点F处.