1. 我国是最早使用正负数表示具有相反意义的量的国家.若向东走60米记作+60米,则向西走80米可记作 ()
A. -80米
B. 0米
C. 80米
D. 140米
A. -80米
B. 0米
C. 80米
D. 140米
答案:
A
2. 下列计算结果为5的是 ()
A. -(+5)
B. +(-5)
C. -(-5)
D. -|-5|
A. -(+5)
B. +(-5)
C. -(-5)
D. -|-5|
答案:
C
3. 计算$\underbrace{3+3+…+3}_{m个3}+\underbrace{4×4×…×4}_{n个4}$的结果是 ()
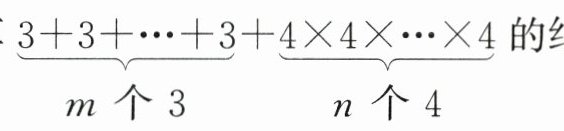
A. $3m + n^4$
B. $m^3 + 4n$
C. $3^m + 4n$
D. $3m + 4^n$
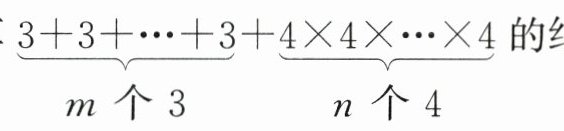
A. $3m + n^4$
B. $m^3 + 4n$
C. $3^m + 4n$
D. $3m + 4^n$
答案:
D
4. 有下列四个等式:①$(-5)+(+3)= -8$;②$-(-2)^3= 6$;③$\left(+\dfrac{5}{6}\right)+\left(-\dfrac{1}{6}\right)= \dfrac{2}{3}$;④$-3÷\left(-\dfrac{1}{3}\right)= 9$.其中,正确的有 ()
A. 0个
B. 1个
C. 2个
D. 3个
A. 0个
B. 1个
C. 2个
D. 3个
答案:
C
5. 福建舰是我国首艘完全自主设计建造的弹射型航空母舰,满载排水量为8万余吨,数据80000用科学记数法表示为 ()
A. $0.8×10^4$
B. $8×10^4$
C. $8×10^5$
D. $0.8×10^5$
A. $0.8×10^4$
B. $8×10^4$
C. $8×10^5$
D. $0.8×10^5$
答案:
B
6. 有理数$a,b,c$在数轴上对应点的位置如图所示,则下列结论正确的是 ()

A. $-c < b$
B. $a > -c$
C. $|a - b| = b - a$
D. $|c - a| = a - c$

A. $-c < b$
B. $a > -c$
C. $|a - b| = b - a$
D. $|c - a| = a - c$
答案:
C
7. 若$-\dfrac{1}{2}x^{m + 3}y与2x^4y^{n + 3}$是同类项,则$(m + n)^{201}$的值为 ()
A. 1
B. 201
C. -1
D. -201
A. 1
B. 201
C. -1
D. -201
答案:
C
8. 已知整式$M:a_nx^n + a_{n - 1}x^{n - 1} + … + a_1x + a_0$,其中$n,a_{n - 1},…,a_0$为自然数,$a_n$为正整数,且$n + a_n + a_{n - 1} + … + a_1 + a_0 = 5$.有下列说法:①满足条件的整式$M$中有5个是单项式;②不存在任何一个$n$,使得满足条件的整式$M$有且只有3个;③满足条件的整式$M$共有16个.其中,正确的个数是 ()
A. 0
B. 1
C. 2
D. 3
A. 0
B. 1
C. 2
D. 3
答案:
D 解析:因为 $ n,a_{n - 1},\cdots,a_0 $ 为自然数,$ a_n $ 为正整数,且 $ n + a_n + a_{n - 1} + \cdots + a_1 + a_0 = 5 $,所以 $ 0 \leq n \leq 4 $。当 $ n = 4 $ 时,$ 4 + a_4 + a_3 + a_2 + a_1 + a_0 = 5 $,所以 $ a_4 = 1 $,$ a_3 = a_2 = a_1 = a_0 = 0 $,满足条件的整式为 $ x^4 $;当 $ n = 3 $ 时,$ 3 + a_3 + a_2 + a_1 + a_0 = 5 $,所以 $ a_3,a_2,a_1,a_0 $ 分别为 $ 2,0,0,0 $ 或 $ 1,1,0,0 $ 或 $ 1,0,1,0 $ 或 $ 1,0,0,1 $,满足条件的整式为 $ 2x^3,x^3 + x^2,x^3 + x,x^3 + 1 $;当 $ n = 2 $ 时,$ 2 + a_2 + a_1 + a_0 = 5 $,所以 $ a_2,a_1,a_0 $ 分别为 $ 3,0,0 $ 或 $ 2,1,0 $ 或 $ 2,0,1 $ 或 $ 1,2,0 $ 或 $ 1,0,2 $ 或 $ 1,1,1 $,满足条件的整式为 $ 3x^2,2x^2 + x,2x^2 + 1,x^2 + 2x,x^2 + 2,x^2 + x + 1 $;当 $ n = 1 $ 时,$ 1 + a_1 + a_0 = 5 $,所以 $ a_1,a_0 $ 分别为 $ 4,0 $ 或 $ 3,1 $ 或 $ 1,3 $ 或 $ 2,2 $,满足条件的整式为 $ 4x,3x + 1,x + 3,2x + 2 $;当 $ n = 0 $ 时,$ 0 + a_0 = 5 $,所以 $ a_0 = 5 $,满足条件的整式为 $ 5 $。综上所述,满足条件的单项式为 $ x^4,2x^3,3x^2,4x,5 $,所以①正确;不存在任何一个 $ n $,使得满足条件的整式 $ M $ 有且只有 $ 3 $ 个,所以②正确;满足条件的整式 $ M $ 共有 $ 1 + 4 + 6 + 4 + 1 = 16 $(个),所以③正确。综上所述,正确的个数是 $ 3 $。
查看更多完整答案,请扫码查看


