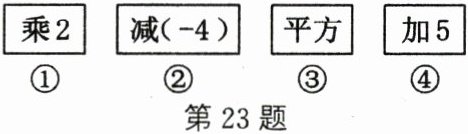
23. (6分)如图,①②③④四张卡片分别代表一种运算.
(1)-3经过①→②→③→④顺序的运算结果是多少?
(2)将$a$经过③→①→④顺序的运算结果记为$A$,将$a - 5$经过④→③→②顺序的运算结果记为$B$,试比较$A与B$的大小,并说明理由.
(1)-3经过①→②→③→④顺序的运算结果是多少?
(2)将$a$经过③→①→④顺序的运算结果记为$A$,将$a - 5$经过④→③→②顺序的运算结果记为$B$,试比较$A与B$的大小,并说明理由.

答案:
(1) 根据题意,得 $ [(-3) \times 2 - (-4)]^2 + 5 = (-6 + 4)^2 + 5 = 4 + 5 = 9 $
(2) $ A > B $ 理由: 根据题意,得 $ A = a^2 \times 2 + 5 = 2a^2 + 5 $,$ B = (a - 5 + 5)^2 - (-4) = a^2 + 4 $。所以 $ A - B = (2a^2 + 5) - (a^2 + 4) = 2a^2 + 5 - a^2 - 4 = a^2 + 1 $。因为 $ a^2 \geq 0 $,所以 $ a^2 + 1 > 0 $。所以 $ A - B > 0 $,即 $ A > B $。
(1) 根据题意,得 $ [(-3) \times 2 - (-4)]^2 + 5 = (-6 + 4)^2 + 5 = 4 + 5 = 9 $
(2) $ A > B $ 理由: 根据题意,得 $ A = a^2 \times 2 + 5 = 2a^2 + 5 $,$ B = (a - 5 + 5)^2 - (-4) = a^2 + 4 $。所以 $ A - B = (2a^2 + 5) - (a^2 + 4) = 2a^2 + 5 - a^2 - 4 = a^2 + 1 $。因为 $ a^2 \geq 0 $,所以 $ a^2 + 1 > 0 $。所以 $ A - B > 0 $,即 $ A > B $。
查看更多完整答案,请扫码查看


