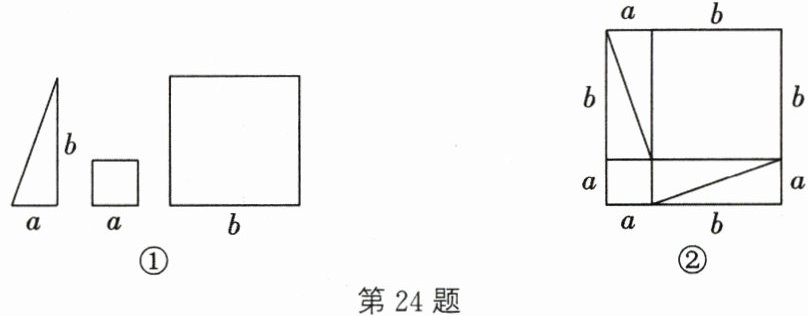
24. (8分)如图①所示为1个直角三角形和2个小正方形,直角三角形的两条直角边的长分别是$a,b$,2个小正方形的边长分别是$a,b(a < b)$.如图②,将4个完全一样的直角三角形和2个小正方形拼成一个大正方形.
(1)用两种不同方法表示图②中大正方形的面积:
方法一:______;
方法二:______.
(2)观察图②,直接写出$(a + b)^2,a^2,b^2,2ab$这四个代数式之间的等量关系,并根据等量关系求$92^2 + 16×92 + 64$的值.
(3)若直角三角形的两条直角边的长均是正整数,且每个直角三角形的面积都为3,求图②中2个小正方形面积的和.
(1)用两种不同方法表示图②中大正方形的面积:
方法一:______;
方法二:______.
(2)观察图②,直接写出$(a + b)^2,a^2,b^2,2ab$这四个代数式之间的等量关系,并根据等量关系求$92^2 + 16×92 + 64$的值.
(3)若直角三角形的两条直角边的长均是正整数,且每个直角三角形的面积都为3,求图②中2个小正方形面积的和.

答案:
(1) $ (a + b)^2 $ $ a^2 + b^2 + 2ab $
(2) $ (a + b)^2 = a^2 + b^2 + 2ab $。$ 92^2 + 16 \times 92 + 64 = 92^2 + 2 \times 8 \times 92 + 8^2 = (92 + 8)^2 = 100^2 = 10000 $
(3) 根据题意,得 $ \frac{1}{2}ab = 3 $,即 $ ab = 6 $。因为 $ a,b $ 均为正整数,所以 $ a = 1,b = 6 $ 或 $ a = 2,b = 3 $。所以 $ a^2 + b^2 = 1 + 36 = 37 $ 或 $ a^2 + b^2 = 4 + 9 = 13 $。所以题图②中 $ 2 $ 个小正方形面积的和为 $ 37 $ 或 $ 13 $
(1) $ (a + b)^2 $ $ a^2 + b^2 + 2ab $
(2) $ (a + b)^2 = a^2 + b^2 + 2ab $。$ 92^2 + 16 \times 92 + 64 = 92^2 + 2 \times 8 \times 92 + 8^2 = (92 + 8)^2 = 100^2 = 10000 $
(3) 根据题意,得 $ \frac{1}{2}ab = 3 $,即 $ ab = 6 $。因为 $ a,b $ 均为正整数,所以 $ a = 1,b = 6 $ 或 $ a = 2,b = 3 $。所以 $ a^2 + b^2 = 1 + 36 = 37 $ 或 $ a^2 + b^2 = 4 + 9 = 13 $。所以题图②中 $ 2 $ 个小正方形面积的和为 $ 37 $ 或 $ 13 $
查看更多完整答案,请扫码查看


