《2025年核心素养天天练三年级数学下册北师大版》

1. 一个长方形，如果宽不变，长增加4分米，面积就增加20平方分米；如果长不变，宽增加3分米，面积就增加18平方分米。原长方形的面积是多少平方分米？
思路分析 根据题意画图（如右图）：由图①可知，原长方形的宽是20÷4 = 5(分米)，由图②可知，原长方形的长是18÷3 = 6(分米)，代入长方形面积公式求解即可。
　　　　　　

答案： 20÷4 = 5(分米) 18÷3 = 6(分米)
6×5 = 30(平方分米)

2. 学校有一块长方形草坪，将一组对边增加了4米，这样就变成一块正方形草坪，面积增加了48平方米，原来长方形草坪的面积是多少平方米？

答案： 48÷4 = 12(米) 12 - 4 = 8(米)
12×8 = 96(平方米)
解析:增加部分的面积是一个宽为4米、长等于原来长方形的长的长方形的面积,因为“长 = 面积÷宽”,据此求出原来的长,原来的宽比长少4米,据此可以求出原来的宽,然后把数据代入公式求出原来长方形的面积。

3. 如图所示，在门前的台阶上铺地毯，已知台阶的宽度为20分米，每平方米地毯40元，那么购买这块地毯一共要多少元？
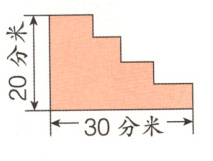
思路分析 台阶表面为不规则图形，可以通过平移的方法把它转化成长方形计算。

答案： 30 + 20 = 50(分米)
50×20 = 1000(平方分米)
1000平方分米 = 10平方米
40×10 = 400(元)
解析:由图可知,通过平移,求出地毯的长度为(20 + 30)分米。用长×宽求出地毯的面积,然后用每平方米地毯的价钱×地毯的面积 = 总价钱。计算时要注意单位统一。

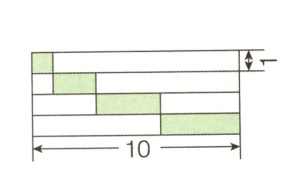
4. 求阴影部分的面积。（单位：厘米）

答案： 1×10 = 10(平方厘米)
解析:通过平移,阴影部分可变成一个长10厘米、宽1厘米的长方形,然后根据面积公式计算即可。

12×30 = 　　　　15×40 = 　　　　248÷2 = 　　　　483÷3 = 　　　　348÷6 =
25×20 = 　　　　60×12 = 　　　　288÷9= 　　　　525÷5 = 　　　　865÷5 =

答案： 口算天天练: 360 600 124 161 58 700 720 32 105 173