第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
问题呈现
961名同学排成一横排,第一次从左到右1至2循环报数,第二次从左到右1至3循环报数,那么每次都报1的同学有多少名?
思路分析
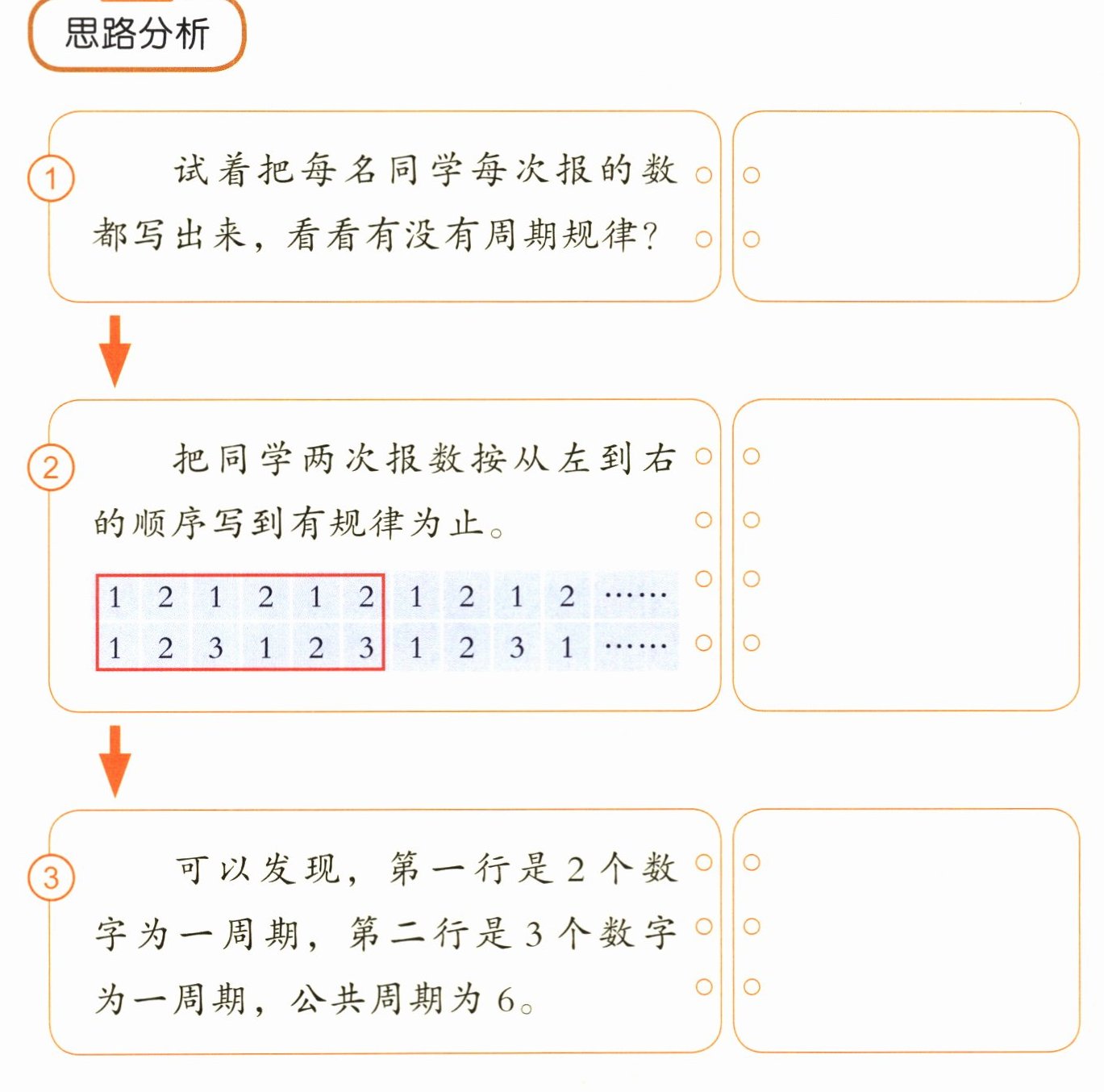
1. 试着把每名同学每次报的数都写出来,看看有没有周期规律?
2. 把同学两次报数按从左到右的顺序写到有规律为止。
|1|2|1|2|1|2|1|2|1|2|……|
|1|2|3|1|2|3|1|2|3|1|……|
3. 可以发现,第一行是2个数字为一周期,第二行是3个数字为一周期,公共周期为6。
4. 可以通过计算得出$961 ÷ 6 = 160 … … 1$,一个周期里只有1名两次均报1的同学,余数里还有1名,共$160 + 1 = 161$(名)。
解题关键
第一种思路,分别根据各自的周期计算结果,最后加以组合;第二种思路,由于公共周期必须同时是两个规律甚至更多规律的周期,所以公共周期的长度必须是这些周期长度的倍数,一般要找最小的那个倍数。
961名同学排成一横排,第一次从左到右1至2循环报数,第二次从左到右1至3循环报数,那么每次都报1的同学有多少名?
思路分析
1. 试着把每名同学每次报的数都写出来,看看有没有周期规律?
2. 把同学两次报数按从左到右的顺序写到有规律为止。
|1|2|1|2|1|2|1|2|1|2|……|
|1|2|3|1|2|3|1|2|3|1|……|
3. 可以发现,第一行是2个数字为一周期,第二行是3个数字为一周期,公共周期为6。

4. 可以通过计算得出$961 ÷ 6 = 160 … … 1$,一个周期里只有1名两次均报1的同学,余数里还有1名,共$160 + 1 = 161$(名)。
解题关键
第一种思路,分别根据各自的周期计算结果,最后加以组合;第二种思路,由于公共周期必须同时是两个规律甚至更多规律的周期,所以公共周期的长度必须是这些周期长度的倍数,一般要找最小的那个倍数。
答案:
查看更多完整答案,请扫码查看


