有一项是符合题目要求的.)
1.设p、q是两个命题,则“复合命题p或q为真,p且q为假”的充要条件是 ( )
A.p、q中至少有一个为真 B.p、q中至少有一个为假
C.p、q中有且只有一个为真 D.p为真,q为假
22.解(1)令m=-1,n=0则:f (–1)=f (–1)f (0),而f (–1)>1 ∴f(0)=1
令m=x>0,n= –x<0则f (x–x)=f (x)·f (–x)=1
∴f (x)=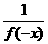
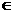 (0,1),即x>0时0<f (x)<1
(0,1),即x>0时0<f (x)<1
设x1<x2则x2–x1=0 ∴0<f (x2–x1)·f (x1)–f (x1)=f (x1)[f (x2–x1)–1]<0 ∴f(x)<f(x1)
即y = f (x)在R上单调递减
(2)由f (an+1)=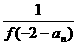 ,n
,n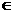 N* 得:f (an+1)·f (–2–an)
=1
N* 得:f (an+1)·f (–2–an)
=1
∴f (an+1–an–2) = f (0) 由(1)知:an+1–an–2=0
即an+1–an=2(n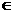 N*) ∴{an}是首项为a1=1,公差为2的等差数列
N*) ∴{an}是首项为a1=1,公差为2的等差数列
∴an=2n–1
(3)假设存在正数k,使(1+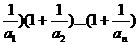
 对n
对n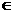 N*恒成立
N*恒成立
记F(n)=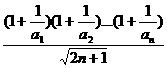
即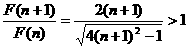 ∴F(n)是递增数列,F(1)为最小值。
∴F(n)是递增数列,F(1)为最小值。
由F(n) 恒成立知k
恒成立知k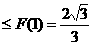 ∴kmax =
∴kmax = 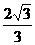 .
.
22.(本小题满分14分)y = f
(x)的定义域为R,对任意实数m、n有f (m+n) =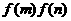 ,且当x<0时,
,且当x<0时, ,数列{an}满足
,数列{an}满足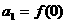 且
且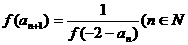 *)。
(1)求证:y = f
(x)在R上单调递减;
(2)求数列{an}的通项公式;
(3)是否存在正数k,使
*)。
(1)求证:y = f
(x)在R上单调递减;
(2)求数列{an}的通项公式;
(3)是否存在正数k,使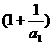 ·
·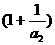 …
…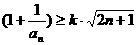 ,对一切n∈N*均成立,若存在,试求出k的最大值并证明,若不存在,说明理由。
,对一切n∈N*均成立,若存在,试求出k的最大值并证明,若不存在,说明理由。
21. 解:(I)由已知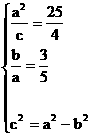 ,解之得:
,解之得: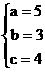 …………(3分)
…………(3分)
∴椭圆的方程为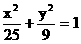 ,双曲线的方程
,双曲线的方程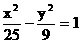
又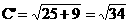
∴双曲线的离心率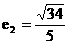 ………………(7分)
………………(7分)
(II)由(I)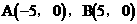
设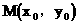 则由
则由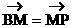 得M为BP的中点
得M为BP的中点
∴P点坐标为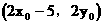
将M、P坐标代入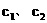 方程得:
方程得:
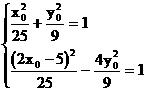
消去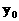 得:
得: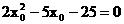
解之得: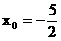 或
或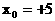 (舍)
(舍)
由此可得: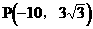 ………………(9分)
………………(9分)
当P为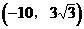 时,
时,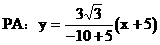
即: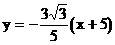
代入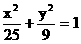 ,得:
,得: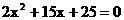
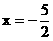 或
或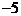 (舍)
(舍)

MN⊥x轴,即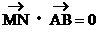 ………………(14分)
………………(14分)
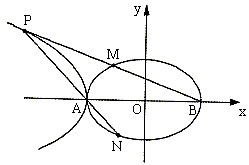
21.(本小题满分12分)已知椭圆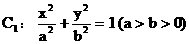 的一条准线方程是
的一条准线方程是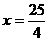 ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线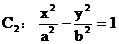 的一条渐近线方程为
的一条渐近线方程为 。
。
(I)求椭圆 的方程及双曲线
的方程及双曲线 的离心率;
的离心率;
(II)在第二象限内取双曲线 上一点P,连结BP交椭圆
上一点P,连结BP交椭圆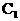 于点M,连结PA并延长交椭圆
于点M,连结PA并延长交椭圆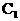 于点N,若
于点N,若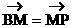 。求证:
。求证: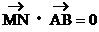 。
。
20. (本小题满分12分)某厂家拟在2005年国庆节期间举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m万元(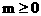 )满足
)满足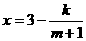 (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2005年生产该产品的固定投入为8
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2005年生产该产品的固定投入为8
万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定
为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分
资金)
(1)将2005年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2005年的促销费用投入多少万元时,厂家的年利润最大?
解:(1)设2005年生产产品x万件
 时,
时,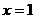 代入
代入
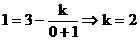 ………………(2分)
………………(2分)
则年成本: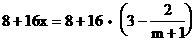 ………………(4分)
………………(4分)
年利润: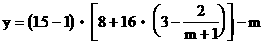 …………(6分)
…………(6分)
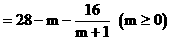 ……………………(7分)
……………………(7分)
(2)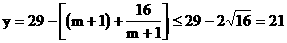 ………………(10分)
………………(10分)
当且仅当 ,即
,即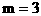 时取等号………………(11分)
时取等号………………(11分)
 时,
时,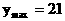 万元……………………(12分)
万元……………………(12分)
19.(本小题满分12分)已知函数 (k为常数),A(-2k, 2)是函数
(k为常数),A(-2k, 2)是函数 图象上的点。
图象上的点。
(I)求实数k的值及函数 的解析式;
的解析式;
(II)将 的图象按向量
的图象按向量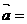 (3,0)平移,得到函数y=g(x)的图象。若
(3,0)平移,得到函数y=g(x)的图象。若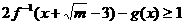 恒成立,试求实数m的取值范围。
恒成立,试求实数m的取值范围。
解:(I)∵A(-2k, 2)是函数y=f-1(x)图象上的点。
∴B(2,-2K)是函数y=f(x)上的点。 ∴2k=32+k
∴k=-3, ∴y=f(x)=3x-3 ∴y=f-1(x)=log3(x+3),(x>-3)
(II)将y=f-1(x)的图象按向量 =(3,0)平移,得函数y=g(x)=log3x(x>0)
=(3,0)平移,得函数y=g(x)=log3x(x>0)
要使2f-1(x+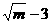 )-g(x)≥1 恒成立, 即使2log3(x+
)-g(x)≥1 恒成立, 即使2log3(x+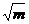 )-log3x≥1恒成立。
)-log3x≥1恒成立。
所以有x+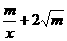 ≥3在x>0时恒成立,只须(x+
≥3在x>0时恒成立,只须(x+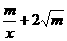 )min≥3。
)min≥3。
又x+ (当且仅当x=
(当且仅当x=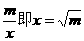 时取等号)
时取等号)
∴(x+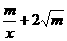 )min=4
)min=4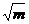 只须4
只须4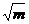 ≥3,即m≥
≥3,即m≥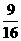 。
。
∴实数m的取值范围为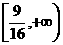

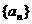 的前n项和为
的前n项和为 ( )
( ) B.
B.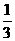 C.
C.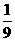 D.
D.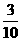
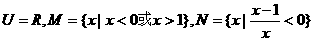 ,则 ( )
,则 ( )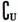
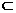
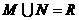 B.
B.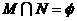 C. N=M D. N M
C. N=M D. N M  ( )
( )