练习册

  • 练习册
  • 试题
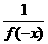
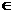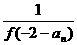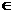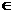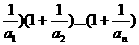
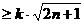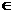    22．解(1)令m=-1.n=0则:f (–1)=f (–1)f (0).而f >1 ∴f(0)=1 令m=x>0.n=­ –x<0则f (x–x)=f (x)·f (–x)=1 ∴f (x)=(0,1).即x>0时0<f (x)<1 设x1<x2则x2–x1=0 ∴0<f (x2–x1)·f (x1)–f (x1)=f (x1)[f (x2–x1)–1]<0 ∴f(x)<f(x1) 即y = f (x)在R上单调递减 (2)由f (an+1)=.nN* 得:f (an+1)·f (–2–an) =1 ∴f (an+1–an–2) = f 知:an+1–an–2=0 即an+1–an=2(nN*) ∴{an}是首项为a1=1.公差为2的等差数列 ∴an=2n–1 (3)假设存在正数k.使(1+对nN*恒成立 记F(n)=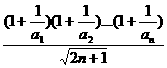 即 ∴F(n)是递增数列.F(1)为最小值. 由F(n)恒成立知k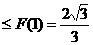 ∴kmax = . 【查看更多】

     

    题目列表(包括答案和解析)

    设定义域为R的函数f(x)=
    |lg|x-1||，x≠1
    0，x=1
    且关于x的方程f2（x）+bf（x）+c=0有7个不同实数解，令m=2010b，n=2010c，则（　　）

    查看答案和解析>>

    设定义域为R的函数f(x)=
    |lg|x-1||，x≠1
    0，x=1
    且关于x的方程f2（x）+bf（x）+c=0有7个不同实数解，令m=2010b，n=2010c，则（　　）
    A．m＜nB．m=n
    C．m＞nD．m，n的大小不确定

    查看答案和解析>>

    已知数列{dn}满足dn=n，等比数列{an}为递增数列，且a52=a10，2（an+an+2）=5an+1，n∈N*．
    （Ⅰ）求an；
    （Ⅱ）令cn=1-（-1）nan，不等式ck≥2014（1≤k≤100，k∈N*）的解集为M，求所有dk+ak（k∈M）的和．

    查看答案和解析>>

    已知数列{an}成等差数列，且a3=11，a6=23，令bn=
    a1+a2+a 3+…+an
    n
    ．
    （1）求数列{bn}的前n项和Sn；
    （2）若Cn=
    1
    Sn
    ，若数列{Cn}的前n项和为Tn，且对任意的n∈N*都有Tn≥m无解，求m范围．

    查看答案和解析>>

    在平行四边形OABC中，已知过点C的直线与线段OA，OB分别相交于点M，N．若
    OM
    =x
    OA
    ，
    ON
    =y
    OB
    ．
    （1）求证：x与y的关系为y=
    x
    x+1
    ；
    （2）设f(x)=
    x
    x+1
    ，定义函数F(x)=
    1
    f(x)
    -1(0＜x≤1)    ，点列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函数F（x）的图象上，且数列{xn}是以首项为1，公比为
    1
    2
    的等比数列，O为原点，令
    OP
    =
    OP1
    +
    OP2
    +…+
    OPn
    ，是否存在点Q（1，m），使得
    OP
    ⊥
    OQ
    ？若存在，请求出Q点坐标；若不存在，请说明理由．
    （3）设函数G（x）为R上偶函数，当x∈[0，1]时G（x）=f（x），又函数G（x）图象关于直线x=1对称，当方程G(x)=ax+
    1
    2
    在x∈[2k，2k+2]（k∈N）上有两个不同的实数解时，求实数a的取值范围．

    查看答案和解析>>


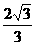    同步练习册答案