2025年PASS教材搭档六年级数学上册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年PASS教材搭档六年级数学上册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
典型例题全解
类型 1 用字母表示图形的面积
例1 如图所示,求阴影部分的面积。
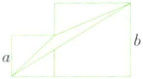
类型 1 用字母表示图形的面积
例1 如图所示,求阴影部分的面积。

答案:
规范解答:阴影部分的面积为两个正方形的面积减去三个直角三角形的面积,
即$S_{阴影} = a^2 + b^2 - \frac{1}{2}(a + b)b - \frac{1}{2}a^2 - \frac{1}{2}(b - a)b$。
即$S_{阴影} = a^2 + b^2 - \frac{1}{2}(a + b)b - \frac{1}{2}a^2 - \frac{1}{2}(b - a)b$。
例2 用字母表示图中阴影部分的面积(其中长方形的长为$a$,宽为2)。

规范解答:把阴影部分的面积转化为长方形与两个圆的一部分面积的差,
即$S_{阴影} = 2 × a - \frac{1}{4} × \pi × 2^2 - \frac{1}{2} × \pi × 1^2 = 2a - \pi - \frac{1}{2} \pi = 2a - \frac{3}{2} \pi$。
类题巧解
解决此类问题的关键是根据图形特点,将所求图形的面积转化为规则图形面积的和与差,用字母分别表示规则图形的面积,最后根据数量关系列出式子。

规范解答:把阴影部分的面积转化为长方形与两个圆的一部分面积的差,
即$S_{阴影} = 2 × a - \frac{1}{4} × \pi × 2^2 - \frac{1}{2} × \pi × 1^2 = 2a - \pi - \frac{1}{2} \pi = 2a - \frac{3}{2} \pi$。
类题巧解
解决此类问题的关键是根据图形特点,将所求图形的面积转化为规则图形面积的和与差,用字母分别表示规则图形的面积,最后根据数量关系列出式子。
答案:
规范解答:把阴影部分的面积转化为长方形与两个圆的一部分面积的差,
即$S_{阴影} = 2 × a - \frac{1}{4} × \pi × 2^2 - \frac{1}{2} × \pi × 1^2 = 2a - \pi - \frac{1}{2} \pi = 2a - \frac{3}{2} \pi$。
类题巧解
解决此类问题的关键是根据图形特点,将所求图形的面积转化为规则图形面积的和与差,用字母分别表示规则图形的面积,最后根据数量关系列出式子。
即$S_{阴影} = 2 × a - \frac{1}{4} × \pi × 2^2 - \frac{1}{2} × \pi × 1^2 = 2a - \pi - \frac{1}{2} \pi = 2a - \frac{3}{2} \pi$。
类题巧解
解决此类问题的关键是根据图形特点,将所求图形的面积转化为规则图形面积的和与差,用字母分别表示规则图形的面积,最后根据数量关系列出式子。
类型 2 用字母表示数的应用
例3
(1) 已知$a$ kg 商品的售价为$p$元,则6 kg该商品的售价为
(2) 温度由$30° C$下降$t° C$后是
(3) 某长方形的长是宽的$\frac{3}{2}$倍,且长是$a$ cm,则该长方形的周长为
(4) 产量由$m$ kg增长10%,就达到
例3
(1) 已知$a$ kg 商品的售价为$p$元,则6 kg该商品的售价为
$\frac{6p}{a}$
元。(2) 温度由$30° C$下降$t° C$后是
$30 - t$
$° C$。(3) 某长方形的长是宽的$\frac{3}{2}$倍,且长是$a$ cm,则该长方形的周长为
$2(a + \frac{2}{3}a)$
cm。(4) 产量由$m$ kg增长10%,就达到
$1.1m$
kg。
答案:
规范解答:
(1) 先求出每千克该商品的售价为$\frac{p}{a}$元,
再求6 kg该商品的售价为$\frac{6p}{a}$元。
(2) 温度由$30° C$下降$t° C$后是$(30 - t)° C$。
(3) 因为长是$a$ cm,长是宽的$\frac{3}{2}$倍,所以宽是$\frac{2}{3}a$ cm,
所以周长为$2(a + \frac{2}{3}a)$ cm。
(4) 产量由$m$ kg增长10%,就达到$(1 + 10\%)m = 1.1m$ (kg)。
答案:
(1) $\frac{6p}{a}$
(2) $30 - t$
(3) $2(a + \frac{2}{3}a)$
(4) $1.1m$
(1) 先求出每千克该商品的售价为$\frac{p}{a}$元,
再求6 kg该商品的售价为$\frac{6p}{a}$元。
(2) 温度由$30° C$下降$t° C$后是$(30 - t)° C$。
(3) 因为长是$a$ cm,长是宽的$\frac{3}{2}$倍,所以宽是$\frac{2}{3}a$ cm,
所以周长为$2(a + \frac{2}{3}a)$ cm。
(4) 产量由$m$ kg增长10%,就达到$(1 + 10\%)m = 1.1m$ (kg)。
答案:
(1) $\frac{6p}{a}$
(2) $30 - t$
(3) $2(a + \frac{2}{3}a)$
(4) $1.1m$
例4
(1) 正方体的棱长为$a$,则其表面积为
(2) 拿100元钱去买钢笔,买了价格为3元/支的钢笔$n$支,则剩下的钱为
(3) 在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是$a$ cm,小正方形的边长是$b$ cm,则剩余部分的面积为
(1) 正方体的棱长为$a$,则其表面积为
$6a^2$
,体积为$a^3$
。(2) 拿100元钱去买钢笔,买了价格为3元/支的钢笔$n$支,则剩下的钱为
$100 - 3n$
元,最多能买这种钢笔33
支。(3) 在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是$a$ cm,小正方形的边长是$b$ cm,则剩余部分的面积为
$a^2 - b^2$
$cm^2$。
答案:
规范解答:
(1) 因为正方体的棱长为$a$,所以它的表面积为$6a^2$,体积为$a^3$。
(2) 买$n$支钢笔用去$3n$元,所以剩下$(100 - 3n)$元。
当$n = 33$,即买33支钢笔时,剩下的钱为$100 - 3 × 33 = 1$(元),所以100元钱最多能买这种钢笔33支。
(3) 由题意知,大正方形的面积为$a^2$ $cm^2$,小正方形的面积为$b^2$ $cm^2$,所以剩余部分的面积为$(a^2 - b^2)$ $cm^2$。
答案:
(1) $6a^2$,$a^3$
(2) $100 - 3n$,33
(3) $a^2 - b^2$
类题巧解
用字母表示数要注意两点:一是要理解日常生活中一些实际问题中的数量关系,如销售问题、增长率问题等;二是要明确常见的图形的周长、面积、体积公式。
(1) 因为正方体的棱长为$a$,所以它的表面积为$6a^2$,体积为$a^3$。
(2) 买$n$支钢笔用去$3n$元,所以剩下$(100 - 3n)$元。
当$n = 33$,即买33支钢笔时,剩下的钱为$100 - 3 × 33 = 1$(元),所以100元钱最多能买这种钢笔33支。
(3) 由题意知,大正方形的面积为$a^2$ $cm^2$,小正方形的面积为$b^2$ $cm^2$,所以剩余部分的面积为$(a^2 - b^2)$ $cm^2$。
答案:
(1) $6a^2$,$a^3$
(2) $100 - 3n$,33
(3) $a^2 - b^2$
类题巧解
用字母表示数要注意两点:一是要理解日常生活中一些实际问题中的数量关系,如销售问题、增长率问题等;二是要明确常见的图形的周长、面积、体积公式。
查看更多完整答案,请扫码查看


