《2025年高中同步单元滚动强化卷高中数学选择性必修第三册人教A版》

1. 已知两条异面直线 $a$，$b$ 上分别有 $5$ 个点和 $8$ 个点，则这 $13$ 个点可以确定不同的平面个数为 (C)

A.$40$
B.$1 624$
C.$13$
D.$10$

答案： 1.C 分两类情况讨论：第1类，直线$a$分别与直线$b$上的
8个点可以确定8个不同的平面；第2类，直线$b$分别与
直线$a$上的5个点可以确定5个不同的平面.根据分类
加法计数原理知，共可以确定$8 + 5 = 13$个不同的平面.
故选C.

2. 用 $0$，$1$，$·s$，$9$ 十个数字，可以组成有重复数字的三位数的个数为 (B)

A.$243$
B.$252$
C.$261$
D.$279$

答案： 2.B 由分步乘法计数原理知，用0,1，$·s$,9十个数字组成
三位数(可有重复数字)的个数为$9 × 10 × 10 = 900$，组成
没有重复数字的三位数的个数为$9 × 9 × 8 = 648$，则组成
有重复数字的三位数的个数为$900 - 648 = 252$.故选B.

3. 下列等式不正确的是 (D)

A.$C_{n}^{m}=\frac{n!}{m!(n - m)!}$
B.$C_{n}^{m}=C_{n}^{n - m}$
C.$C_{n}^{m}=\frac{m + 1}{n + 1}C_{n + 1}^{m + 1}$
D.$C_{n}^{m}=C_{n + 1}^{m + 1}$

答案： 3.D 因为$C_{n + 1}^{m + 1} = \frac{(n + 1)!}{(m + 1)!(n - m)!} = \frac{n + 1}{m + 1} · \frac{n!}{m!(n - m)!}$
$\neq C_{n}^{m}$，所以D不正确.故选D.

4. 身穿红、黄两种颜色衣服的各有 $2$ 人，身穿蓝颜色衣服的有 $1$ 人，现将这 $5$ 人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法共有 (D)

A.$24$ 种
B.$28$ 种
C.$36$ 种
D.$48$ 种

答案： 4.D 由题意知，先是5个人的全排列，共有$A_{5}^{5}$种排法，
去掉身穿相同颜色衣服的人都相邻的情况，再去掉仅身
穿红色衣服的人相邻和仅身穿黄色衣服的人相邻两种
情况.所以身穿相同颜色衣服的人不能相邻的排法有
$A_{5}^{5} - A_{2}^{2}A_{2}^{2}A_{3}^{3} - 2A_{2}^{2}A_{2}^{2}A_{2}^{2} = 48$种.故选D.

5. 某市拟从 $4$ 个重点项目和 $6$ 个一般项目中各选 $2$ 个项目作为本年度要启动的项目，则重点项目 $A$ 和一般项目 $B$ 至少有一个被选中的不同选法的种数是 (C)

A.$15$
B.$45$
C.$60$
D.$75$

答案： 5.C 从4个重点项目和6个一般项目中各选2个项目作
为本年度要启动的项目，所有的选法种数是$C_{4}^{2} × C_{6}^{2} =$
90.重点项目A和一般项目B都没有被选中的选法种
数是$C_{3}^{2} × C_{5}^{2} = 30$，故重点项目A和一般项目B至少有
一个被选中的不同选法种数是$90 - 30 = 60$.故选C.

6. 已知 $a$，$b\in\{0,1,2,·s,9\}$，若满足 $|a - b|\leq1$，则称 $a$，$b$“心有灵犀”。则 $a$，$b$“心有灵犀”的情形共有 (D)

A.$9$ 种
B.$16$ 种
C.$20$ 种
D.$28$ 种

答案： 6.D 当$a$为0时，$b$只能取0,1两个数；当$a$为9时，$b$只
能取8,9两个数；当$a$为其他数时，$b$都可以取3个数.
故共有$2 + 2 + 8 × 3 = 28$种情形.故选D.

7. 在春节来临之际，甲、乙、丙、丁、戊、戌 $6$ 个人都计划回家过春节，现打算从 $A$，$B$，$C$，$D$ 四个航空公司中任选一个购买回家的机票，其中甲和丙是老乡，他俩选择在同一个航空公司购买机票，丁不选 $B$ 航空公司，则四个航空公司均有人选的购票方案种数为 (C)

A.$132$
B.$162$
C.$180$
D.$204$

答案： 7.C 当有1个人选择B航空公司时，购票方案共有
$C_{4}^{1}(C_{3}^{1}C_{3}^{2}A_{2}^{2} + C_{3}^{1}C_{3}^{2}A_{2}^{2}) = 108$种；当有2个人选择B航
空公司时，购票方案共有$C_{4}^{2}A_{3}^{3} + C_{3}^{2}A_{3}^{3} = 54$种；当有3
个人选择B航空公司时，购票方案共有$C_{4}^{3}A_{3}^{3} = 18$种.
故四个航空公司均有人选的购票方案共有$108 + 54 +$
$18 = 180$种.故选C.

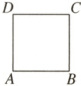
8. 某人设计一项单人游戏，规则如下：先将一棋子放在如图所示正方形 $ABCD$(边长为 $2$ 个单位)的顶点 $A$ 处，然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位，如果掷出的点数为 $i(i = 1,2,·s,6)$，则棋子就按逆时针方向行走 $i$ 个单位，一直循环下去。则某人抛掷三次骰子后棋子恰好又回到点 $A$ 处的所有不同走法共有 (D)

A.$22$ 种
B.$24$ 种
C.$25$ 种
D.$27$ 种

答案： 8.D 由题意知，正方形$ABCD$(边长为2个单位)的周长
是8个单位，抛掷三次骰子后棋子恰好又回到点$A$处，
表示三次骰子的点数之和是8或16，点数和为8或16
的有125,134,116,224,233,466,556，共有7种组合.组
合125,134，每种情况可以排列出$A_{3}^{3} = 6$种走法，共有
$2A_{3}^{3} = 2 × 6 = 12$种走法；组合116,224,233,466,556各
自可以列出3种走法，共有$5 × 3 = 15$种走法.根据分类
加法计数原理知，共有$12 + 15 = 27$种走法.故选D.

9. $A$，$B$，$C$，$D$，$E$ 五个人并排站在一起，则下列说法正确的有 (BCD)

A.若 $A$，$B$ 两人站在一起，有 $24$ 种排法
B.若 $A$，$B$ 不相邻，共有 $72$ 种排法
C.若 $A$ 在 $B$ 左边，有 $60$ 种排法
D.若 $A$ 不站在最左边，$B$ 不站在最右边，有 $78$ 种排法

答案： 9.BCD 对于选项A，先将$A,B$排列，再看成一个元素，
和剩余的3人，一共4个元素进行全排列，由分步乘法
计数原理可知共有$A_{2}^{2}A_{4}^{4} = 48$种，所以A不正确.对于
选项B，先将$A,B$之外的3人全排列，产生4个空，再将
$A,B$两元素插空，所以共有$A_{3}^{3}A_{4}^{2} = 72$种，所以B正确.
对于选项C，5人全排列，而其中$A$在$B$的左边和$A$在
$B$的右边是等可能的，所以$A$在$B$的左边的排法有
$\frac{1}{2}A_{5}^{5} = 60$种，所以C正确.对于选项D，对$A$分两种情
况：一种是若$A$站在最右边，则剩下的4人全排列有$A_{4}^{4}$
种排法；另一种是$A$不站在最左边也不站在最右边，则
$A$从中间的3个位置中任选1个，然后剩下3人全排列即可，由
分类加法计数原理可知，共有$A_{4}^{4} + C_{3}^{1}C_{3}^{1}A_{3}^{3} = 78$种排
法，所以D正确.故选B、C、D.