《2025年高中同步单元滚动强化卷高中数学选择性必修第三册人教A版》

10. 下列说法正确的是(ABD)

A.设随机变量 $ X $ 服从二项分布 $ B(6,\frac{1}{2}) $，则 $ P(X = 3) = \frac{5}{16} $
B.已知随机变量 $ X $ 服从正态分布 $ N(2,\sigma^{2}) $ 且 $ P(X ＜ 4) = 0.9 $，则 $ P(0 ＜ X ＜ 2) = 0.4 $
C.$ E(2X + 3) = 2E(X) + 3 $，$ D(2X + 3) = 2D(X) + 3 $
D.已知随机变量 $ \xi $ 满足 $ P(\xi = 0) = x $，$ P(\xi = 1) = 1 - x $，若 $ 0 ＜ x ＜ \frac{1}{2} $，则 $ E(\xi) $ 随着 $ x $ 的增大而减小，$ D(\xi) $ 随着 $ x $ 的增大而增大

答案： 10.ABD 对于选项A，因为随机变量X服从二项分布$B(6,\frac{1}{2})$，所以$P(X = 3)=C_{6}^{3}×(\frac{1}{2})^{3}×(1 - \frac{1}{2})^{3}=\frac{5}{16}$，故A正确.对于选项B，因为随机变量X服从正态分布$N(2,\sigma^{2})$，所以正态曲线的对称轴是$x = 2$.又$P(X＜4)=0.9$，所以$P(0＜X＜4)=0.8$，所以$P(0＜X＜2)=P(2＜X＜4)=0.4$，故B正确.对于选项C，$E(2X + 3)=2E(X)+3$，$D(2X + 3)=4D(X)$，故C错误.对于选项D，$E(\xi)=1 - x$，$D(\xi)=x(1 - x)= - x^{2}+x$，由一次函数和二次函数的性质知，当$0＜x＜\frac{1}{2}$时，$E(\xi)$随着x的增大而减小，$D(\xi)$随着x的增大而增大，故D正确.故选A、B、D.

11. 下列说法正确的是(BCD)

A.已知随机变量 $ X $ 服从二项分布 $ B(n,p) $，若 $ E(X) = 30 $，$ D(X) = 20 $，则 $ p = \frac{2}{3} $
B.已知 $ A_{n}^{3} = C_{n}^{4} $，则 $ n = 27 $
C.设随机变量 $ \xi $ 服从正态分布 $ N(0,1) $，若 $ P(\xi ＞ 1) = p $，则 $ P(-1 ＜ \xi ＜ 0) = \frac{1}{2} - p $
D.某人在 10 次射击中，击中目标的次数为 $ X $，$ X \sim B(10,0.8) $，则当 $ X = 8 $ 时概率最大

答案： 11.BCD 对于选项A，由随机变量X服从二项分布$B(n,p)$，$E(X)=30$，$D(X)=20$，得$np = 30$，$np(1 - p)=20$，解得$p=\frac{1}{3}$，故A错误.对于选项B，易知$n\geq4$，且$n\in N^{*}$，$A_{n}^{3}=\frac{n!}{(n - 3)!}=n(n - 2)(n - 1)$，$C_{n}^{4}=\frac{n!}{4!(n - 4)!}=\frac{n(n - 3)(n - 2)(n - 1)}{24}$，由$A_{n}^{3}=C_{n}^{4}$，得$n(n - 2)(n - 1)=\frac{n(n - 3)(n - 2)(n - 1)}{24}$，即$\frac{n - 3}{24}=1$，解得$n = 27$，故B正确.对于选项C，随机变量$\xi$服从正态分布$N(0,1)$，则对应的正态曲线关于y轴对称，若$P(\xi＞1)=p$，则$P(0＜\xi＜1)=\frac{1}{2}-p$，即$P(-1＜\xi＜0)=\frac{1}{2}-p$，故C正确.对于选项D，由$X\sim B(10,0.8)$，得当$X = k(0\leq k\leq10$，且$k\in N)$时，$P(X = k)=C_{10}^{k}·0.8^{k}·0.2^{10 - k}$，所以当$k\geq1$时，$\frac{P(X = k)}{P(X = k - 1)}=\frac{C_{10}^{k}·0.8^{k}·0.2^{10 - k}}{C_{10}^{k - 1}·0.8^{k - 1}·0.2^{10 - k + 1}}=\frac{4(11 - k)}{k}$，由$\frac{P(X = k)}{P(X = k - 1)}\geq1$，得$44 - 4k\geq k$，即$1\leq k\leq\frac{44}{5}$，因为$k\in N$，所以$1\leq k\leq8$且$k\in N$，即$k = 8$时，概率$P(X = k)$最大，故D正确.故选B、C、D.

12. 5 件产品中，有 3 件一等品和 2 件二等品，从中任取 2 件，那么以 $\frac{7}{10}$ 为概率的事件是至多有1件一等品。

答案： 12.解析：$P(都不是一等品)=\frac{C_{3}^{0}C_{7}^{2}}{C_{10}^{2}}=\frac{1}{10}$，$P(恰有1件一等品)=\frac{C_{3}^{1}C_{7}^{1}}{C_{10}^{2}}=\frac{6}{10}$，$P(都是一等品)=\frac{C_{3}^{2}}{C_{10}^{2}}=\frac{3}{10}$，$P(至少有1件一等品)=1-\frac{1}{10}=\frac{9}{10}$，$P(至多有1件一等品)=1-\frac{C_{3}^{2}}{C_{10}^{2}}=\frac{7}{10}$.
答案：至多有1件一等品

13. 有 10 件产品，其中 3 件是次品，从中任取 2 件。若 $ X $ 表示取得次品的个数，则 $ P(X ＜ 2) = $$\frac{14}{15}$，随机变量 $ X $ 的数学期望 $ E(X) = $$\frac{3}{5}$。

答案： 13.解析：由题意可知，X表示取得次品的个数，则X服从超几何分布，所以$P(X＜2)=\frac{C_{3}^{0}C_{7}^{2}}{C_{10}^{2}}+\frac{C_{3}^{1}C_{7}^{1}}{C_{10}^{2}}=\frac{14}{15}$，$E(X)=0×\frac{C_{3}^{0}C_{7}^{2}}{C_{10}^{2}}+1×\frac{C_{3}^{1}C_{7}^{1}}{C_{10}^{2}}+2×\frac{C_{3}^{2}C_{7}^{0}}{C_{10}^{2}}=\frac{3}{5}$.
答案：$\frac{14}{15}$ $\frac{3}{5}$

14. 已知某公司生产的一种产品的质量 $ X $(单位：克)服从正态分布 $ N(100,4) $。现从该产品的生产线上随机抽取 10000 件产品，其中质量在 $[98,104]$ 内的产品数量估计为8186。
附：若 $ X $ 服从 $ N(\mu,\sigma^{2}) $，则 $ P(\mu - \sigma \leq X \leq \mu + \sigma) \approx 0.6827 $，$ P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) \approx 0.9545 $。

答案： 14.解析：由题意可得，该正态分布对应的曲线关于直线$x = 100$对称，且$\sigma = 2$，则质量在$[96,104]$内的产品的概率为$P(\mu - 2\sigma\leq X\leq\mu + 2\sigma)\approx0.9545$，而质量在$[98,102]$内的产品的概率为$P(\mu - \sigma\leq X\leq\mu + \sigma)\approx0.6827$，结合正态曲线的对称性可知，质量在$[98,104]$内的产品的概率约为$0.6827+\frac{0.9545 - 0.6827}{2}=0.8186$，据此估计质量在$[98,104]$内的产品的数量为$10000×0.8186 = 8186$.
答案：8186

15.（13 分）设随机变量 $ X \sim N(2,9) $，若 $ P(X ＞ c + 1) = P(X ＜ c - 1) $。
(1) 求 $ c $ 的值；
(2) 求 $ P(-4 \leq X \leq 8) $。
附：若 $ X $ 服从 $ N(\mu,\sigma^{2}) $，则 $ P(\mu - \sigma \leq X \leq \mu + \sigma) \approx 0.6827 $，$ P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) \approx 0.9545 $。

答案：
15.解：
(1)由$X\sim N(2,9)$可知，正态曲线关于直线$x = 2$对称(如图所示)，

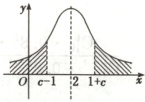
由$P(X＞c + 1)=P(X＜c - 1)$，得$2-(c - 1)=(c + 1)-2$，所以$c = 2$.
(2)$P(-4\leq X\leq8)=P(2 - 2×3\leq X\leq2 + 2×3)\approx0.9545$.