2025年高中同步单元滚动强化卷高中数学选择性必修第三册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中同步单元滚动强化卷高中数学选择性必修第三册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 某班有 28 名男生,22 名女生,从中选一名同学作为数学课代表,则不同的选法有(
A.28 种
B.22 种
C.50 种
D.616 种
C
)A.28 种
B.22 种
C.50 种
D.616 种
答案:
1.C 由分类加法计数原理可知,共有$28 + 22 = 50$种不同的选法.故选C.
2. 某食堂备有 6 种荤菜,5 种素菜,3 种汤。现要配制“一荤,一素,一汤”的套餐,则可以配制的不同套餐的种数为(
A.14
B.90
C.18
D.15
B
)A.14
B.90
C.18
D.15
答案:
2.B 由分步乘法计数原理得,共有$6 × 5 × 3 = 90$种不同的配制方法.故选B.
3. 数列$\{ a_{n}\}$共有六项,其中四项均为 1,其余两项各不相同,则满足上述条件的数列$\{ a_{n}\}$共有(
A.30 个
B.31 个
C.60 个
D.61 个
A
)A.30 个
B.31 个
C.60 个
D.61 个
答案:
3.A 在数列$\{ a_{n}\}$的六项中,只要考虑两个非$1$的项的位置,即得不同数列,共有$A_{6}^{2} = 30$个不同的数列.故选A.
4. $A_{4}^{2}-C_{3}^{2}$等于(
A.9
B.12
C.15
D.3
A
)A.9
B.12
C.15
D.3
答案:
4.A $A_{4}^{2} - C_{3}^{3} = 4 × 3 - \frac{3 × 2}{2 × 1} = 12 - 3 = 9$.故选A.
5. 在$(x^{2}-\frac {1}{x})^{5}$的二项展开式中,第 2 项的系数为(
A.10
B.$-10$
C.5
D.$-5$
D
)A.10
B.$-10$
C.5
D.$-5$
答案:
5.D 展开式中的第$2$项为$T_{2} = C_{5}^{1}(x^{2})^{5 - 1}( - \frac{1}{x})^{1}$,所以其系数为$- C_{5}^{1} = - 5$.故选D.
6. 用 4 种不同的颜色涂图中的矩形 $A$,$B$,$C$,$D$,若要求有公共边界的矩形涂色不同,则不同涂法有(
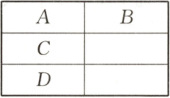
A.72 种
B.48 种
C.24 种
D.108 种
D
)
A.72 种
B.48 种
C.24 种
D.108 种
答案:
6.D 涂A共$4$种涂法,则涂B有$3$种涂法,涂C有$3$种涂法,涂D有$3$种涂法,所以共有$4 × 3 × 3 × 3 = 108$种涂法.故选D.
7. 设$(3x+\frac {1}{x})^{n}$展开式的各项系数之和为 $M$,其二项式系数之和为 $N$。若 $M + N = 272$,则 $n$的值为(
A.1
B.4
C.3
D.$\frac {1}{2}$
B
)A.1
B.4
C.3
D.$\frac {1}{2}$
答案:
7.B 由题意,得$M = 4^{n}$,$N = 2^{n}$.因为$M + N = 272$,所以$4^{n} + 2^{n} = 272$,解得$n = 4$.故选B.
8. 某电路图如图,在 $A$,$B$ 间有 4 个开关。若发现 $A$,$B$ 之间电路不通,则这 4 个开关打开或闭合的方式有(
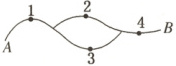
A.3 种
B.8 种
C.13 种
D.16 种
C
)
A.3 种
B.8 种
C.13 种
D.16 种
答案:
8.C 每个开关都有打开或闭合这$2$种情形,故这$4$个开关共有$2 × 2 × 2 × 2 = 16$种可能,其中能使电路接通的情形有$1,4$都闭合,且$2$和$3$中至少有一个闭合,共有$3$种可能,故电路不通时,开关打开或闭合的不同情形共有$16 - 3 = 13$种.故选C.
9. 若 $C_{8}^{m - 1} \gt 3C_{8}^{m}$,则 $m$的取值可能是(
A.6
B.7
C.8
D.9
BC
)A.6
B.7
C.8
D.9
答案:
9.BC 根据题意,对于$C_{m - 1}^{n - 1} > 3C_{m}^{n}$,有$0 \leq m - 1 \leq 8$且$0 \leq m \leq 8$,则有$1 \leq m \leq 8$,若$C_{m - 1}^{n - 1} > 3C_{m}^{n}$,则有$\frac{8!}{(m - 1)! · (9 - m)!} > 3 × \frac{8!}{m! · (8 - m)!}$,整理,得$m > 27 - 3m$,解得$m > \frac{27}{4}$.综上,$\frac{27}{4} < m \leq 8$,因为$m \in \mathbf{N}^{*}$,所以$m = 7$或$m = 8$.故选B、C.
10. $(1 + ax + by)^{n}$的展开式中不含 $y$的项的系数的绝对值的和为 32,则 $a$,$n$的值可能为(
A.$a = 2$,$n = 5$
B.$a = 1$,$n = 6$
C.$a = -1$,$n = 5$
D.$a = 1$,$n = 5$
CD
)A.$a = 2$,$n = 5$
B.$a = 1$,$n = 6$
C.$a = -1$,$n = 5$
D.$a = 1$,$n = 5$
答案:
10.CD $(1 + ax + by)^{n}$的展开式可以看成$n$个$(1 + ax + by)$相乘,每个$(1 + ax + by)$中取$1,ax,by$之一求得乘积构成的每一项,$(1 + ax + by)^{n}$的展开式中不含$y$的项的系数的绝对值的和为$32$,即$C_{n}^{0} + C_{n}^{1}|a| + C_{n}^{2}|a|^{2} + ·s + C_{n}^{n}|a|^{n} = 32$,即$(1 + |a|)^{n} = 32$,结合四个选项,则$a,n$的值可能为$a = - 1,n = 5$,或$a = 1,n = 5$.故选C、D.
查看更多完整答案,请扫码查看


