《2025年高中同步单元滚动强化卷高中数学选择性必修第三册人教A版》

16. （15分）某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕，基地员工一天可以完成一处种植区的采摘，下雨会影响药材品质，基地收益如下表所示：

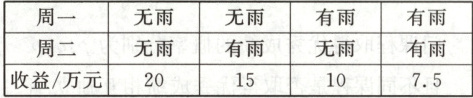
若该基地额外聘请工人，可在下周一当天完成全部采摘任务.无雨时收益为20万元；有雨时收益为10万元.额外聘请工人的成本为$a$万元.已知下周一和下周二有雨的概率相同，两天是否下雨互不影响，基地收益为20万元的概率为0.36.
(1) 若不额外聘请工人，写出基地收益$X$的分布列及该基地的期望收益.
(2) 该基地是否应该额外聘请工人？请说明理由.

答案： 16.解：
(1)设下周一无雨的概率为 $p$，由题意，得 $p^2=0.36$，解得 $p=0.6$(负值已舍去)，该基地收益 $X$ 的可能取值为 20,15,10,7.5，则 $P(X=20)=0.36,P(X=15)=0.24,P(X=10)=0.24$，$P(X=7.5)=0.16$，所以该基地收益 $X$ 的分布列为
$X$ 20 15 10 7.5
$P$ 0.36 0.24 0.24 0.16
$E(X)=20×0.36+15×0.24+10×0.24+7.5×0.16=14.4$，
所以该基地的预期收益为 14.4 万元.
(2)设该基地额外聘请工人时的收益为 $Y$ 万元，
则其期望收益 $E(Y)=20×0.6+10×0.4-a=16-a$，
$E(Y)-E(X)=1.6-a$.
综上，当额外聘请工人的成本高于 1.6 万元时，不额外
聘请工人；当额外聘请工人的成本低于 1.6 万元时，额
外聘请工人；当额外聘请工人的成本恰为 1.6 万元时，
额外聘请或不聘请工人均可以.

17. （15分）甲、乙两人为了响应政府“节能减排”的号召，决定各购置一辆纯电动汽车.经了解，目前市场上销售的主流纯电动汽车，按行驶里程数$R$（单位：千米）可分为三类车型，分别是A：$80 \leq R ＜ 150$；B：$150 \leq R ＜ 250$；C：$R \geq 250$.甲从A、B、C三类车型中挑选，乙从B、C两类车型中挑选，甲、乙二人选择各类车型的概率如下表：

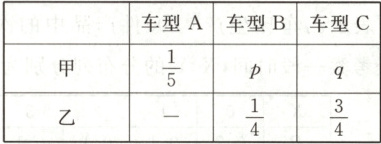
若甲、乙都选C类车型的概率为$\frac{3}{10}$.
(1) 求$p,q$的值.
(2) 求甲、乙选择不同车型的概率.
(3) 该市对购买纯电动汽车进行补贴，补贴标准如下表：

记甲、乙两人购车所获得的财政补贴的和为$X$，求$X$的分布列.

答案： 17.解：
(1)由题意可知，$\begin{cases}\frac{3}{4}q=\frac{3}{10},\\p+q+\frac{1}{5}=1,\end{cases}$ 解得 $p=\frac{2}{5},q=\frac{2}{5}$.
(2)设“甲、乙选择不同车型”为事件 $A$，
则 $P(A)=\frac{1}{5}+\frac{2}{5}×\frac{1}{4}+\frac{2}{5}×\frac{3}{4}=\frac{3}{5}$，
所以甲、乙选择不同车型的概率是 $\frac{3}{5}$.
(3)$X$ 的可能取值为 7,8,9,10，则
$P(X=7)=\frac{1}{5}×\frac{1}{4}=\frac{1}{20}$，
$P(X=8)=\frac{1}{5}×\frac{3}{4}+\frac{2}{5}×\frac{1}{4}=\frac{1}{4}$，
$P(X=9)=\frac{2}{5}×\frac{1}{4}+\frac{2}{5}×\frac{3}{4}=\frac{2}{5}$，
$P(X=10)=\frac{2}{5}×\frac{3}{4}=\frac{3}{10}$，
所以 $X$ 的分布列为
$X$ 7 8 9 10
$P$ $\frac{1}{20}$ $\frac{1}{4}$ $\frac{2}{5}$ $\frac{3}{10}$