2025年新坐标同步练习高中生物选择性必修2人教版青海专用
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中生物选择性必修2人教版青海专用 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 建构数学模型的目的:①
描述
、解释和②预测
种群数量的变化。
答案:
①描述 ②预测
2. 数学模型的概念:用来描述一个③
系统
或它的④性质
的数学形式。
答案:
③系统 ④性质
4. 建构方法和实例
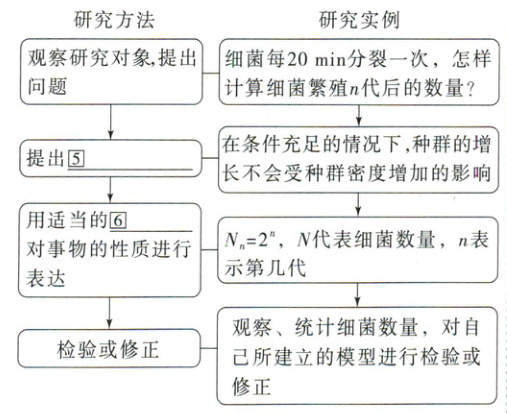

答案:
⑤合理的假设 ⑥数学形式
>辨正误
(1) 数学公式和曲线图都是数学模型的表现形式。(
(2) 数学模型只能用来描述种群数量的变化。(
(1) 数学公式和曲线图都是数学模型的表现形式。(
√
)(2) 数学模型只能用来描述种群数量的变化。(
×
)
答案:
(1)√
(2)× 数学模型不仅可以描述种群数量的变化,还能解释和预测种群数量的未来趋势。
(1)√
(2)× 数学模型不仅可以描述种群数量的变化,还能解释和预测种群数量的未来趋势。
[探究] 下表是一个细菌在营养和生存空间不受限制的条件下,在不同时间产生后代的数量,据表回答下列有关问题:

(1) 填写上表:计算一个细菌在不同时间产生后代的数量。
(2) 第n代细菌数量的计算公式是______。
(3) 72 h后,由一个细菌分裂产生的细菌数量是______个。
(4) 若该种群数量增长一直持续下去,需要满足的条件是______。
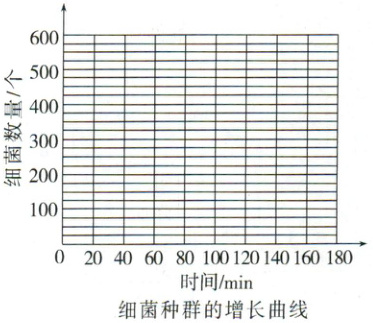
(5) 以时间为横坐标、细菌数量为纵坐标,请在下面坐标图中画出细菌的数量增长曲线。

(1) 填写上表:计算一个细菌在不同时间产生后代的数量。
(2) 第n代细菌数量的计算公式是______。
(3) 72 h后,由一个细菌分裂产生的细菌数量是______个。
(4) 若该种群数量增长一直持续下去,需要满足的条件是______。
(5) 以时间为横坐标、细菌数量为纵坐标,请在下面坐标图中画出细菌的数量增长曲线。

答案:
(1)32 128 256
(2)$N_{n}=2^{n}$
(3)$2^{216}$
(4)理想的实验室条件下,即细菌生活所需的资源和空间无限等
(5)如下图所示
(1)32 128 256
(2)$N_{n}=2^{n}$
(3)$2^{216}$
(4)理想的实验室条件下,即细菌生活所需的资源和空间无限等
(5)如下图所示

查看更多完整答案,请扫码查看


