第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 圆心决定圆的( ),半径决定圆的( )。
答案:
位置,大小
先根据半径确定圆规两脚间的距离,然后把圆规有针尖的脚固定在一点上,最后将装有铅笔(铅笔芯)的脚旋转一周。
- 圆的周长:
围成圆的曲线的长是圆的周长。
圆的周长 = 直径 × 圆周率 $C = \pi d$
- 圆的周长 = 半径 ×( )× 圆周率 $C = 2\pi r$
- 圆的面积:
-
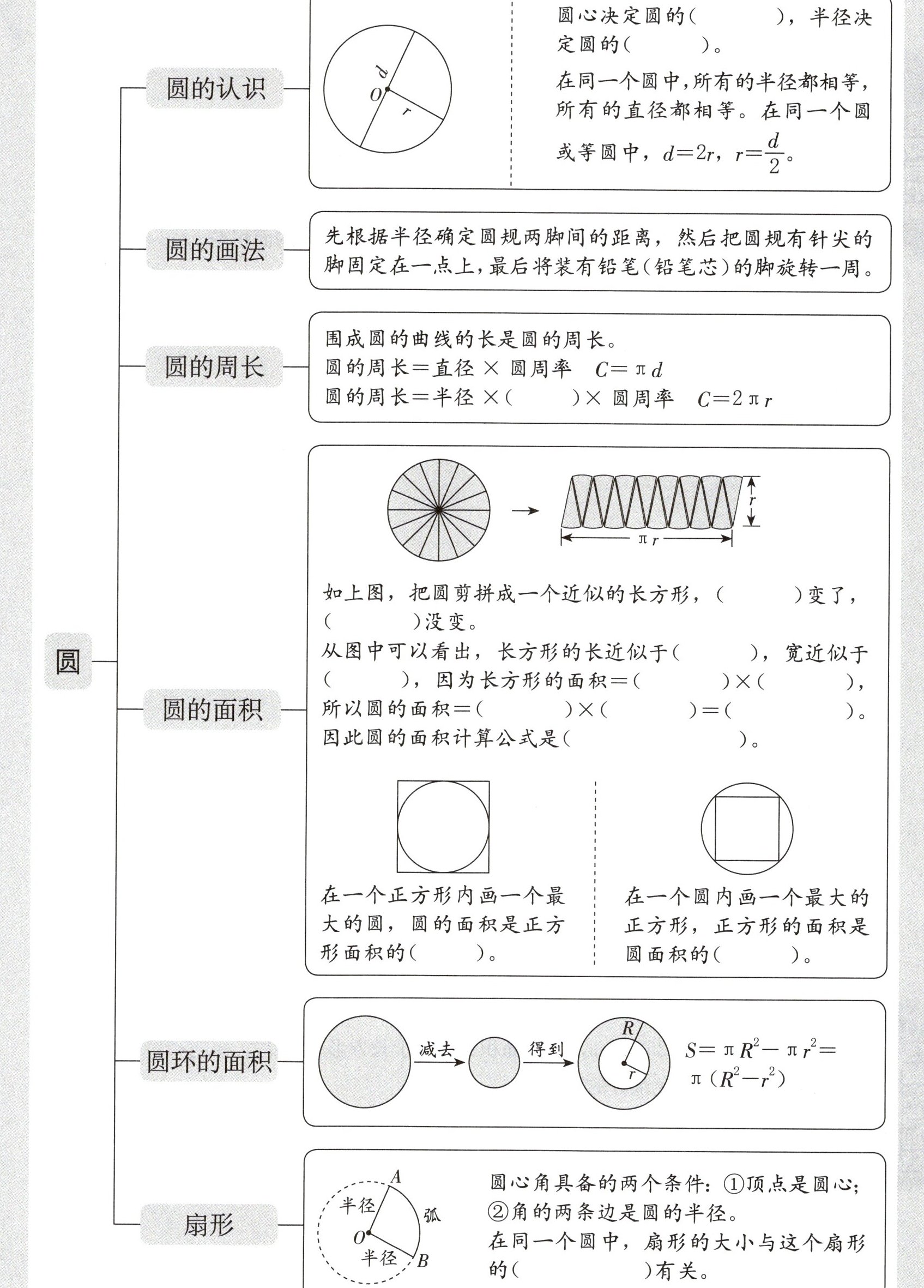
如上图,把圆剪拼成一个近似的长方形,( )变了,( )没变。
从图中可以看出,长方形的长近似于( ),宽近似于( ),因为长方形的面积 = ( )×( ),所以圆的面积 = ( )×( )= ( )。因此圆的面积计算公式是( )。
- 圆的周长:
围成圆的曲线的长是圆的周长。
圆的周长 = 直径 × 圆周率 $C = \pi d$
- 圆的周长 = 半径 ×( )× 圆周率 $C = 2\pi r$
- 圆的面积:
-
如上图,把圆剪拼成一个近似的长方形,( )变了,( )没变。
从图中可以看出,长方形的长近似于( ),宽近似于( ),因为长方形的面积 = ( )×( ),所以圆的面积 = ( )×( )= ( )。因此圆的面积计算公式是( )。

答案:
$2$;形状;面积;圆周长的一半;半径;长;宽;$\pi r$;$r$;$\pi r^{2}$;$S = \pi r^{2}$
先根据半径确定圆规两脚间的距离,然后把圆规有针尖的脚固定在一点上,最后将装有铅笔(铅笔芯)的脚旋转一周。
- 圆的周长:
围成圆的曲线的长是圆的周长。
圆的周长 = 直径 × 圆周率 $C = \pi d$
- 圆的周长 = 半径 ×(
- 圆的面积:
-
如上图,把圆剪拼成一个近似的长方形,(
从图中可以看出,长方形的长近似于(

- 圆的周长:
围成圆的曲线的长是圆的周长。
圆的周长 = 直径 × 圆周率 $C = \pi d$
- 圆的周长 = 半径 ×(
2
)× 圆周率 $C = 2\pi r$- 圆的面积:
-
如上图,把圆剪拼成一个近似的长方形,(
形状
)变了,(面积
)没变。从图中可以看出,长方形的长近似于(
圆周长的一半
),宽近似于(圆的半径
),因为长方形的面积 = (长
)×(宽
),所以圆的面积 = (πr
)×(r
)= (πr²
)。因此圆的面积计算公式是(S=πr²
)。
答案:
2;形状;面积;圆周长的一半;圆的半径;长;宽;πr;r;πr²;S=πr²
- 在一个正方形内画一个最大的圆,圆的面积是正方形面积的( )。
答案:
π/4
- 在一个圆内画一个最大的正方形,正方形的面积是圆面积的( )。
答案:
2/π
- 在同一个圆中,扇形的大小与这个扇形的( )有关。
答案:
圆心角
查看更多完整答案,请扫码查看


