《2025年精彩练习就练这一本九年级科学全一册浙教版评议教辅》

6. 如图所示，小宁组装了甲、乙两种滑轮，用来提升同一物体，该物体重为$400N$(不计绳重、滑轮重和摩擦)。将物体沿竖直方向匀速提升$1m$，下列说法正确的是(D)


A.$F_{甲}=400N$，施力处向上移动$2m$
B.$F_{甲}=200N$，施力处向上移动$1m$
C.$F_{乙}=400N$，施力处向上移动$0.5m$
D.$F_{乙}=800N$，施力处向上移动$0.5m$

答案： D

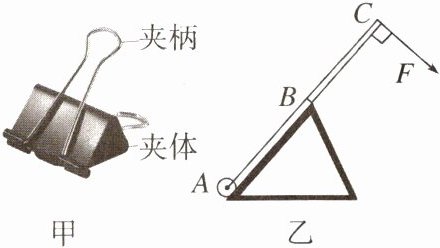
7. 图甲所示的燕尾夹包括夹柄和夹体，夹体的截面为三角形。夹柄是钢丝制成，与夹体相连接的一端可活动，燕尾夹夹柄可简化为杠杆$ABC$，其中$AB = BC$，以图乙方式按住$C$点打开该燕尾夹，力$F$垂直于夹柄所在平面。
杠杆$ABC$的支点为B(填“$A$”“$B$”或“$C$”)。
若当$F$大小为$10N$时刚好可以打开该燕尾夹，则夹体给杠杆的作用力至少为多少？
在不改变夹体的前提下，为能更轻松地打开该燕尾夹，可以使用什么办法？请列式说明理由。

答案：
(1)B
解:
(2)当力F垂直于燕尾夹夹柄所在平面时,动力臂是BC,阻力臂是AB,由题可知$AB=BC$,即动力臂等于阻力臂,此时动力与阻力相等,若当F大小为10 N时刚好可以打开夹子,则夹体给杠杆的作用力最小是10 N。
(3)由杠杆的平衡条件可得:$F_{1}L_{1}=F_{2}L_{2}$,在不改变夹体的前提下,阻力和阻力臂都不变,为能更轻松地打开该燕尾夹,即减小动力,应该使动力臂BC部分加长,且在C点用力时,力的方向垂直于BC。

8. 如图甲所示，物体在拉力$F$作用下，沿长$L$、高$H$、粗糙程度不变的斜面向上运动(不考虑空气的阻力)，物体上升高度$H$与时间$t$的关系图像如图乙所示，$0$至$t_{1}$时间内的拉力为$F_{1}$，$t_{1}$至$t_{2}$时间内的拉力为$F_{2}$。不计速度变化所用的时间。请回答下列问题。


若斜面的长度$L$为$5m$，将物体匀速拉至顶端的拉力为$18N$，则拉力做的功为90J。
物体在斜面上运动时，受到的拉力大于(填“大于”“小于”或“等于”)摩擦力。
比较拉力为$F_{1}$时的斜面机械效率$\eta_{1}$和拉力为$F_{2}$时的斜面机械效率$\eta_{2}$的大小关系，并用学过的知识推导。

答案：
(1)90
(2)大于
(3)$\eta_{1}=\eta_{2}$
推导:$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{GH}{FL}×100\%=\frac{GH}{GH+fL}×100\%=\frac{1}{1+\frac{fL}{GH}}×100\%$,
斜面倾斜角度一定,所以物体沿斜面运动的路程L与上升的高度H的比值是一定的,即$\frac{L}{H}$为定值;斜面的粗糙程度不变,物体对斜面的压力不变,物体运动过程中摩擦力不变;物体重力不变,所以机械效率相等,即$\eta_{1}=\eta_{2}$。