《2025年预学与导学七年级科学上册浙教版》

5. 如图所示的量筒是以mL为单位标度的,最小刻度是2mL。读数时若视线如图所示,则读出的液体体积与真实值相比偏大(填“偏大”“偏小”或“相等”),正确的读数为24mL。

答案： 【解析】：
本题考查量筒的使用和读数方法，量筒上标有$mL$单位，是用来测量液体体积的仪器。
从图中可以看出，量筒每$10mL$之间有$5$个小格，所以每个小格表示$2mL$，即最小刻度为$2mL$。
读数时，视线应与液面的凹液面最低处相平，图中视线是俯视，俯视读数会使读出的液体体积比真实值偏大。
正确的读数方法是视线与凹液面最低处相平，此时读数为$24mL$。
【答案】：
$mL$；$2mL$；偏大；$24mL$

6. 一个量筒和一个量杯的量程都是 100 毫升(设底部到最大量程的高度都是 h)。如果倒入 50 毫升的液体,对量筒而言,所装液体的液面高度将等于$\frac{h}{2}$；对量杯而言,液面高度将大于$\frac{h}{2}$。如果它们的最小刻度都是 5 毫升,那么当所测液体体积较大时,选用量筒测量更准确。

答案： 【解析】：
本题主要考查了量筒和量杯的结构特点以及测量准确性的判断。
首先，需要理解量筒和量杯的结构差异。量筒的刻度是均匀的，这意味着液体的体积与液面的高度成正比。因此，当倒入50毫升的液体时，液面的高度将是量筒最大量程高度h的一半，即$\frac{h}{2}$。而量杯的刻度则是不均匀的，通常上密下疏，这是为了更精确地测量小体积的液体。当倒入50毫升的液体时，由于量杯的刻度特点，液面的高度会大于其最大量程高度h的一半，即大于$\frac{h}{2}$。
其次，需要考虑测量的准确性。当所测液体体积较大时，如果刻度间隔大，那么测量的误差就会相对较大。由于量筒的刻度是均匀的，且刻度间隔相对较小（特别是与量杯相比，在大量程时），因此使用量筒进行测量会更准确。
【答案】：
等于；大于；量筒。

7. 完成下列单位换算。
(1)120 立方分米=0.12立方米=120000立方厘米。
(2)2.7 升=2700毫升=0.0027立方米。
(3)2450 立方厘米=2.45立方分米=0.00245立方米。
(4)0.5 立方米=500000立方厘米=500000毫升=500升。

答案： 【解析】：
本题主要考察单位换算，特别是体积和容量的单位之间的换算。
我们需要知道以下单位换算关系：
$1立方米 = 1000立方分米$
$1立方分米 = 1000立方厘米$
$1升 = 1000毫升$
$1升 = 1立方分米$
$1毫升 = 1立方厘米$
(1) 对于$120$立方分米，换算成立方米，就是$120 ÷ 1000 = 0.12$立方米；
换算成立方厘米，就是$120 × 1000 = 120000$立方厘米。
(2) 对于$2.7$升，换算成毫升，就是$2.7 × 1000 = 2700$毫升；
换算成立方米，就是$2.7 ÷ 1000 = 0.0027$立方米（因为$1$升$ = 1$立方分米，所以也可以先换算成$2.7$立方分米再换算成立方米）。
(3) 对于$2450$立方厘米，换算成立方分米，就是$2450 ÷ 1000 = 2.45$立方分米；
换算成立方米，就是$2.45 ÷ 1000 = 0.00245$立方米。
(4) 对于$0.5$立方米，换算成立方厘米，就是$0.5 × 1000 × 1000 = 500000$立方厘米；
换算成毫升，就是$500000$毫升（因为$1$立方厘米 $= 1$毫升）；
换算成升，就是$500000 ÷ 1000 = 500$升。
【答案】：
(1) $0.12$；$120000$
(2) $2700$；$0.0027$
(3) $2.45$；$0.00245$
(4) $500000$；$500000$；$500$

8. 填上合适的体积单位。
(1)一瓶矿泉水的体积为 596mL（或 毫升）。
(2)一大瓶可乐的体积为 2.5L（或 升）。
(3)一间教室的容积约为 200$m^3$（或 立方米）。
(4)一台冰箱的容积约为 560L（或 升）。

答案： 【解析】：
本题主要考察对生活中常见物体体积或容积的估测以及单位的选择。需要根据对体积和容积单位的理解，结合生活常识，为给定的物体选择合适的体积或容积单位。
(1)一瓶矿泉水的体积通常不会太大，因此常用的单位是毫升(mL)。所以，一瓶矿泉水的体积为596mL是合理的。
(2)一大瓶可乐的体积相对较大，但仍然使用升(L)作为单位更为恰当，因为毫升单位对于大体积来说不太方便。所以，一大瓶可乐的体积为2.5L是合适的。
(3)一间教室的容积很大，因此使用立方米($m^3$)作为单位是合适的。所以，一间教室的容积约为200$m^3$是合理的。
(4)一台冰箱的容积适中，既不会太大也不会太小，因此使用升(L)作为单位是恰当的。但需要注意的是，在实际生活中，冰箱的容积也常用“升”的倍数或小数来表示，且题目中给出的数字560更适合用“升”来表示，而不是更大的或更小的单位。所以，一台冰箱的容积约为560L是合理的，但考虑到冰箱容积的常规表示方法，这里更可能是指“升”的近似值或常规表示，实际上冰箱的容积用“立方分米”（$dm^3$），且$1dm^3 = 1L$，所以填“升”或“立方分米”均可，但在此情境下，“升”更为常用。
【答案】：
(1)mL（或 毫升）
(2)L（或 升）
(3)$m^3$（或 立方米）
(4)L（或 升）

9. 为了测量漂浮在水面上的蜡块体积,小明想出了如图所示的测量方法。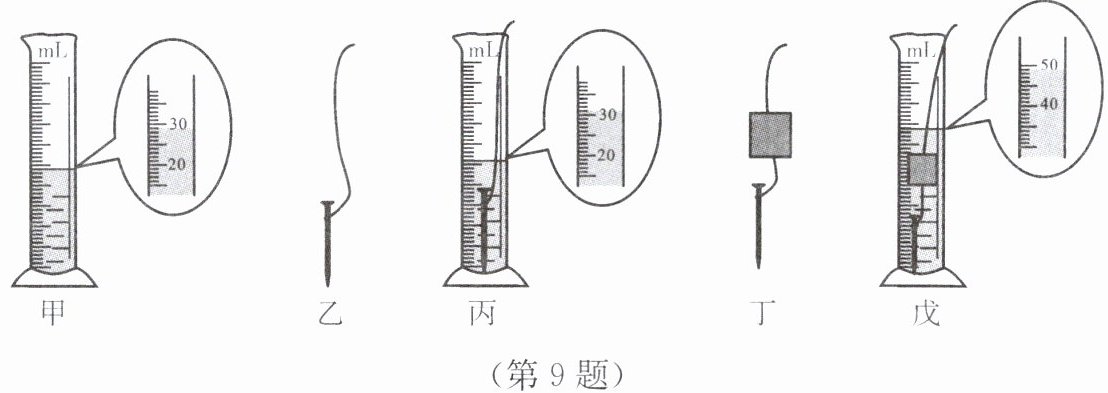
A. 在量筒中倒入适量的水测出体积,如图甲所示。
B. 将一枚铁钉用绳系好,如图乙所示。
C. 将铁钉缓慢浸没于水中,测出体积,如图丙所示。
D. 将蜡块固定在铁钉附近,如图丁所示。
E. 使铁钉和蜡块均浸没在水中,测出体积,如图戊所示。
综合以上步骤即可求出蜡块的体积。请回答下列问题：
(1)A、C、E 三个步骤中都有体积的测量,就测量蜡块体积来说,其中不必要的是A。
(2)根据信息可得蜡块的体积为20cm³。
(3)为了提高实验的精确程度,可改进的措施有选用分度值更小的量筒(写出一点即可)。

答案： 【解析】：
(1)漂浮在水面上的蜡块，其体积就等于浸没蜡块时总体积减掉只浸没铁钉时总体积，就测量蜡块体积来说，A步骤中在量筒中倒入适量的水，测出体积，是不必要的。
(2)由图可知，只浸没铁钉时总体积为$25mL$，浸没铁钉和蜡块时总体积为$45mL$，则蜡块的体积为$45mL - 25mL = 20mL = 20cm^{3}$。
(3)为了提高实验的精确程度，可改进的措施有：选用分度值更小的量筒等。
【答案】：
(1)A
(2)$20cm^{3}$
(3)选用分度值更小的量筒