第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 测一测家里一些物品的体积(容积)。
| 物品 | 体积 | 物品 | 体积 |
| | | | |
| | | | |
| | | | |

| 物品 | 体积 | 物品 | 体积 |
| | | | |
| | | | |
| | | | |

答案:
【解析】:
本题主要考查科学测量中物品体积的测量方法,对于规则形状的物品,可通过测量其长、宽、高,再利用相应体积公式计算;对于不规则形状的物品,可借助量筒,采用排水法来测量其体积,即先在量筒中倒入适量水,记录此时水的体积$V_1$,再将物品浸没在水中,记录此时水和物品的总体积$V_2$,那么物品的体积$V = V_2 - V_1$。
【答案】:
| 物品 | 体积 | 物品 | 体积 |
| --- | --- | --- | --- |
| 示例:正方体木块 | 边长为$a$,体积$V = a^3$(实际测量边长代入计算) | 示例:小石块 | 用排水法,量筒中原来水体积$V_1$,放入石块后总体积$V_2$,体积$V = V_2 - V_1$ |
本题主要考查科学测量中物品体积的测量方法,对于规则形状的物品,可通过测量其长、宽、高,再利用相应体积公式计算;对于不规则形状的物品,可借助量筒,采用排水法来测量其体积,即先在量筒中倒入适量水,记录此时水的体积$V_1$,再将物品浸没在水中,记录此时水和物品的总体积$V_2$,那么物品的体积$V = V_2 - V_1$。
【答案】:
| 物品 | 体积 | 物品 | 体积 |
| --- | --- | --- | --- |
| 示例:正方体木块 | 边长为$a$,体积$V = a^3$(实际测量边长代入计算) | 示例:小石块 | 用排水法,量筒中原来水体积$V_1$,放入石块后总体积$V_2$,体积$V = V_2 - V_1$ |
2. 家庭饲养观赏鱼不仅可以陶冶情操,还能为家居环境带来生机和活力。小李家有一个长方体鱼缸,里面盛了一些水,水里养有一条鱼,如图所示。如果把这条鱼捉出来,水面便会下降一些。现在小李手上只有一把刻度尺,请帮他测出这条鱼的体积。


答案:
【解析】:
本题主要考查如何通过测量水面高度变化来计算不规则物体的体积,涉及到长方体体积公式的应用,即$V = S× h$($V$是体积,$S$是底面积,$h$是高)。
用刻度尺测出鱼缸的长$a$和宽$b$,根据长方体底面积公式$S = a× b$计算出鱼缸的底面积。
把鱼在水中时水面到达的位置在鱼缸外壁上做一个记号,然后将鱼捞出,再测量此时水面到达的高度$h_1$,接着测量鱼在水中时水面到达的高度$h_2$,那么水面下降的高度$\Delta h=h_2 - h_1$。
根据长方体体积公式$V = S×\Delta h=a× b×(h_2 - h_1)$,就可以计算出鱼的体积。
【答案】:
①用刻度尺测出鱼缸的长$a$和宽$b$,算出底面积$S = a× b$;
②测出鱼在水中时水面高度$h_2$,捞出鱼后测出水面高度$h_1$,算出水面下降的高度$\Delta h=h_2 - h_1$;
③鱼的体积$V = a× b×(h_2 - h_1)$。
本题主要考查如何通过测量水面高度变化来计算不规则物体的体积,涉及到长方体体积公式的应用,即$V = S× h$($V$是体积,$S$是底面积,$h$是高)。
用刻度尺测出鱼缸的长$a$和宽$b$,根据长方体底面积公式$S = a× b$计算出鱼缸的底面积。
把鱼在水中时水面到达的位置在鱼缸外壁上做一个记号,然后将鱼捞出,再测量此时水面到达的高度$h_1$,接着测量鱼在水中时水面到达的高度$h_2$,那么水面下降的高度$\Delta h=h_2 - h_1$。
根据长方体体积公式$V = S×\Delta h=a× b×(h_2 - h_1)$,就可以计算出鱼的体积。
【答案】:
①用刻度尺测出鱼缸的长$a$和宽$b$,算出底面积$S = a× b$;
②测出鱼在水中时水面高度$h_2$,捞出鱼后测出水面高度$h_1$,算出水面下降的高度$\Delta h=h_2 - h_1$;
③鱼的体积$V = a× b×(h_2 - h_1)$。
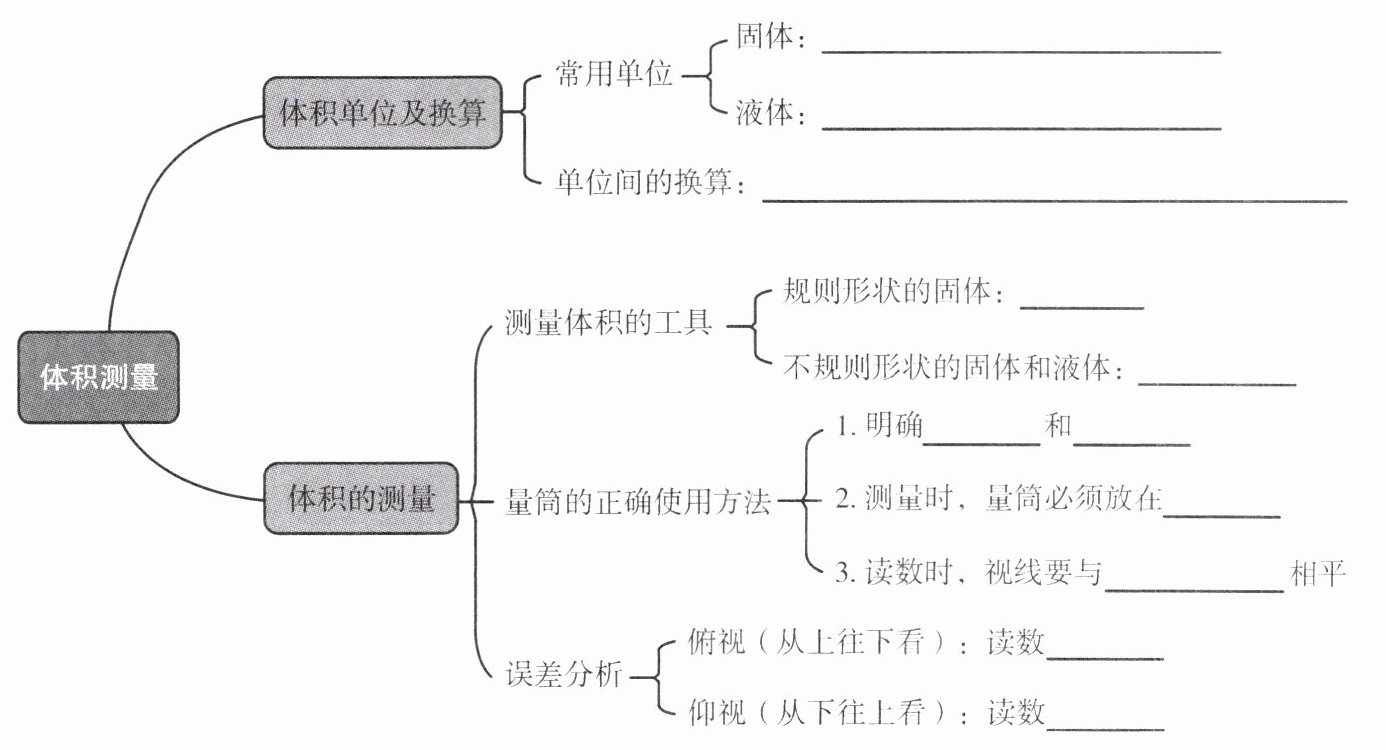
体积测量
├─体积单位及换算
│ ├─常用单位
│ │ ├─固体:
│ │ └─液体:
│ └─单位间的换算:
└─体积的测量
├─测量体积的工具
│ ├─规则形状的固体:
│ └─不规则形状的固体和液体:
├─量筒的正确使用方法
│ ├─1. 明确
│ ├─2. 测量时,量筒必须放在
│ └─3. 读数时,视线要与
└─误差分析
├─俯视(从上往下看):读数
└─仰视(从下往上看):读数
├─体积单位及换算
│ ├─常用单位
│ │ ├─固体:
立方米、立方分米、立方厘米
│ │ └─液体:
升、毫升
│ └─单位间的换算:
1立方米=1000立方分米,1立方分米=1000立方厘米,1升=1立方分米,1毫升=1立方厘米
└─体积的测量
├─测量体积的工具
│ ├─规则形状的固体:
刻度尺
│ └─不规则形状的固体和液体:
量筒(或量杯)
├─量筒的正确使用方法
│ ├─1. 明确
量程
和分度值
│ ├─2. 测量时,量筒必须放在
水平桌面上
│ └─3. 读数时,视线要与
凹液面的最低处(或凸液面的最高处)
相平└─误差分析
├─俯视(从上往下看):读数
偏大
└─仰视(从下往上看):读数
偏小

答案:
固体:立方米、立方分米、立方厘米
液体:升、毫升
单位间的换算:1立方米=1000立方分米,1立方分米=1000立方厘米,1升=1立方分米,1毫升=1立方厘米
规则形状的固体:刻度尺
不规则形状的固体和液体:量筒(或量杯)
1. 量程;分度值
2. 水平桌面上
3. 凹液面的最低处(或凸液面的最高处)
俯视(从上往下看):读数偏大
仰视(从下往上看):读数偏小
液体:升、毫升
单位间的换算:1立方米=1000立方分米,1立方分米=1000立方厘米,1升=1立方分米,1毫升=1立方厘米
规则形状的固体:刻度尺
不规则形状的固体和液体:量筒(或量杯)
1. 量程;分度值
2. 水平桌面上
3. 凹液面的最低处(或凸液面的最高处)
俯视(从上往下看):读数偏大
仰视(从下往上看):读数偏小
查看更多完整答案,请扫码查看


