2025年暑假生活北京师范大学出版社高一物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高一物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
知识点一 圆周运动的运动学问题
1. 匀速圆周运动
(1)定义:如果物体沿着圆周运动,并且线速度的大小处处
(2)特点:加速度大小
(3)条件:合力大小
2. 描述圆周运动的物理量
(1)线速度:大小$v= $
(2)角速度$ω=$
(3)周期:做匀速圆周运动的物体,运动一周所用的时间,$T= $
(4)转速:做匀速圆周运动的物体转动的圈数与所用时间之比,$n= $
(5)向心加速度大小$a_{n}= $
1. 匀速圆周运动
(1)定义:如果物体沿着圆周运动,并且线速度的大小处处
相等
,这种运动叫作匀速圆周运动.(2)特点:加速度大小
不变
,方向始终指向圆心
,是变加速运动.(3)条件:合力大小
不变
、方向始终与速度
方向垂直且指向圆心.2. 描述圆周运动的物理量
(1)线速度:大小$v= $
$\frac{\Delta s}{\Delta t}$
$=$$\frac{2\pi r}{T}$
,方向沿圆周的切线
方向.(2)角速度$ω=$
$\frac{\Delta \theta}{\Delta t}$
$=$$\frac{2\pi}{T}$
;描述做圆周运动的物体绕圆心转动
的快慢.(3)周期:做匀速圆周运动的物体,运动一周所用的时间,$T= $
$\frac{2\pi}{\omega}$
$=$$\frac{2\pi r}{v}$
.(4)转速:做匀速圆周运动的物体转动的圈数与所用时间之比,$n= $
$\frac{1}{T}$
.(5)向心加速度大小$a_{n}= $
$\frac{v^{2}}{r}$
$=$$\omega^{2}r$
$=$$\frac{4\pi^{2}}{T^{2}}r$
$=$$\omega v$
,方向始终指向圆心
.
答案:
1.
(1)相等
(2)不变 圆心
(3)不变 速度 2.
(1)$\frac{\Delta s}{\Delta t}$ $\frac{2\pi r}{T}$ 切线
(2)$\frac{\Delta \theta}{\Delta t}$ $\frac{2\pi}{T}$ 转动
(3)$\frac{2\pi}{\omega}$ $\frac{2\pi r}{v}$
(4)$\frac{1}{T}$
(5)$\frac{v^{2}}{r}$ $\omega^{2}r$ $\frac{4\pi^{2}}{T^{2}}r$ $\omega v$ 圆心
(1)相等
(2)不变 圆心
(3)不变 速度 2.
(1)$\frac{\Delta s}{\Delta t}$ $\frac{2\pi r}{T}$ 切线
(2)$\frac{\Delta \theta}{\Delta t}$ $\frac{2\pi}{T}$ 转动
(3)$\frac{2\pi}{\omega}$ $\frac{2\pi r}{v}$
(4)$\frac{1}{T}$
(5)$\frac{v^{2}}{r}$ $\omega^{2}r$ $\frac{4\pi^{2}}{T^{2}}r$ $\omega v$ 圆心
知识点二 圆周运动的动力学问题
1. 匀速圆周运动的向心力
(1)作用效果:向心力产生向心加速度,只能改变速度的
(2)大小:$F_{n}=$
(3)方向:始终沿半径方向指向
(4)来源:向心力可以由一个力提供,也可以由几个力的
2. 离心运动和近心运动
(1)离心运动:做圆周运动的物体,在所受合力突然消失或不足以提供做圆周运动所需的向心力的情况下,就做
(2)受力特点(如图3-1所示)

①当$F= 0$时,物体沿
②当$0\lt F\lt mω^{2}r$时,物体逐渐
③当$F>mω^{2}r$时,物体逐渐
(3)本质:离心运动的本质并不是受到离心力的作用,而是提供的力
3. 变速圆周运动合力与向心力的特点
做变速圆周运动的物体所受的合力方向一般不指向圆心,可以分解为如下两个分力,如图3-2所示.
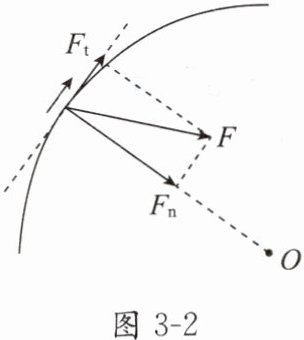
(1)切向分力$F_{t}$:产生切向加速度$a_{t}$,只改变线速度的大小;当$a_{t}与v$同向时,速度增大,做加速圆周运动,反向时则速度减小,做减速圆周运动.
(2)指向圆心的分力$F_{n}$:提供向心力,产生向心加速度$a_{n}$,只改变线速度的
1. 匀速圆周运动的向心力
(1)作用效果:向心力产生向心加速度,只能改变速度的
方向
,不能改变速度的大小
.(2)大小:$F_{n}=$
$ma_{n}$
=$m\frac{v^{2}}{r}$
=$m\omega^{2}r$
=$m\frac{4\pi^{2}}{T^{2}}r$
$=4mπ^{2}n^{2}r= mωv$.(3)方向:始终沿半径方向指向
圆心
,时刻在改变,即向心力是一个变力.(4)来源:向心力可以由一个力提供,也可以由几个力的
合力
提供,还可以由一个力的分力
提供.2. 离心运动和近心运动
(1)离心运动:做圆周运动的物体,在所受合力突然消失或不足以提供做圆周运动所需的向心力的情况下,就做
逐渐远离圆心
的运动.(2)受力特点(如图3-1所示)

①当$F= 0$时,物体沿
切线
方向飞出,做匀速直线运动.②当$0\lt F\lt mω^{2}r$时,物体逐渐
远离
圆心,做离心
运动.③当$F>mω^{2}r$时,物体逐渐
靠近
圆心,做近心
运动.(3)本质:离心运动的本质并不是受到离心力的作用,而是提供的力
小于
做匀速圆周运动需要的向心力.3. 变速圆周运动合力与向心力的特点
做变速圆周运动的物体所受的合力方向一般不指向圆心,可以分解为如下两个分力,如图3-2所示.

(1)切向分力$F_{t}$:产生切向加速度$a_{t}$,只改变线速度的大小;当$a_{t}与v$同向时,速度增大,做加速圆周运动,反向时则速度减小,做减速圆周运动.
(2)指向圆心的分力$F_{n}$:提供向心力,产生向心加速度$a_{n}$,只改变线速度的
方向
.
答案:
1.
(1)方向 大小
(2)$ma_{n}$ $m\frac{v^{2}}{r}$ $m\omega^{2}r$ $m\frac{4\pi^{2}}{T^{2}}r$
(3)圆心
(4)合力 分力 2.
(1)逐渐远离圆心
(2)①切线 ②远离 离心 ③靠近 近心
(3)小于 3.
(2)方向
(1)方向 大小
(2)$ma_{n}$ $m\frac{v^{2}}{r}$ $m\omega^{2}r$ $m\frac{4\pi^{2}}{T^{2}}r$
(3)圆心
(4)合力 分力 2.
(1)逐渐远离圆心
(2)①切线 ②远离 离心 ③靠近 近心
(3)小于 3.
(2)方向
查看更多完整答案,请扫码查看


