《2025年暑假生活北京师范大学出版社高一物理人教版》

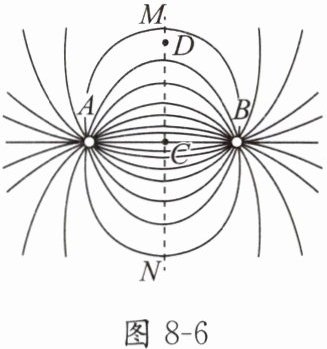
6. $ A $、$ B $ 两个点电荷在真空中产生电场的电场线(方向未标出)如图 8 - 6 所示. 图中 $ C $ 点为两点电荷连线的中点, $ MN $ 为两点电荷连线的中垂线, $ D $ 为中垂线上的一点, 电场线的分布关于 $ MN $ 左右对称. 则下列说法中正确的是( B ).


A.这两个点电荷一定是同种电荷
B.这两个点电荷一定是异种电荷
C.$ D $、$ C $ 两点电场强度相等
D.$ C $ 点的电场强度与 $ D $ 点的电场强度方向不同

答案： B　解析:由题图可知，电场线关于中垂线对称，两点电荷一定是等量异种电荷，选项A错误，选项B正确；中垂线上，C点电场强度最大，离C点越远，电场强度越小，选项C错误；C、D两点的电场强度方向都垂直于中垂线指向同一方向，选项D错误。

7. 如图 8 - 7 所示, 直角三角形 $ ABC $ 中 $ \angle B = 30^{\circ} $, 点电荷 $ A $、$ B $ 所带电荷量分别为 $ Q_A $、$ Q_B $, 测得在 $ C $ 处的某正点电荷所受静电力方向平行于 $ A $、$ B $ 连线向左, 则下列说法正确的是( ).


A.$ A $ 带正电, $ Q_A : Q_B = 1 : 8 $
B.$ A $ 带负电, $ Q_A : Q_B = 1 : 8 $
C.$ A $ 带正电, $ Q_A : Q_B = 1 : 4 $
D.$ A $ 带负电, $ Q_A : Q_B = 1 : 4 $

答案：
B　解析:要使C处的正点电荷所受静电力方向平行于A、B连线向左，该正点电荷所受静电力的情况应如答图8 - 2所示，所以A带负电，B带正电。设A、C间的距离为l，则$F_{B}\sin30^{\circ}=F_{A}$，即$k\frac{Q_{B}Q_{C}}{(2l)^{2}}\sin30^{\circ}=k\frac{Q_{A}Q_{C}}{l^{2}}$，解得$\frac{Q_{A}}{Q_{B}}=\frac{1}{8}$，选项B正确。

8. 如图 8 - 8 所示, 真空中有 $ A $、$ B $、$ C $、$ D $ 四个点在同一直线上, $ AB = BC = CD = d $, 在 $ A $、$ C $ 两点各放置一个点电荷, 其中位于 $ C $ 点的点电荷带电荷量为 $ q(q ＜ 0) $, 已知 $ D $ 点的电场强度为零, 静电力常量为 $ k $, 则 $ B $ 点的电场强度为(D).
A.$ \frac{8kq}{d^2} $, 方向由 $ C $ 指向 $ B $
B.$ \frac{8kq}{d^2} $, 方向由 $ B $ 指向 $ C $
C.$ \frac{10kq}{d^2} $, 方向由 $ C $ 指向 $ B $
D.$ \frac{10kq}{d^2} $, 方向由 $ B $ 指向 $ C $

答案： D　解析:由于D点的电场强度为零，可知位于A点的点电荷带正电，设其带电荷量为Q，则有$k\frac{Q}{(3d)^{2}}=k\frac{q}{d^{2}}$，可知$Q = 9q$；则B点的电场强度$E_{B}=k\frac{9q}{d^{2}}+k\frac{q}{d^{2}}=k\frac{10q}{d^{2}}$，方向由B指向C，故选项D正确。

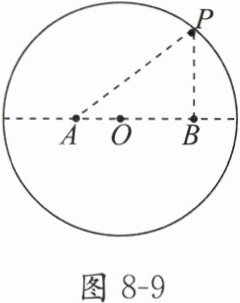
9. (2023·海南卷) 如图 8 - 9 所示, 一光滑绝缘轨道水平放置, 直径上有 $ A $、$ B $ 两点, $ l_{AO} = 2 \text{cm} $, $ l_{OB} = 4 \text{cm} $, 在 $ A $、$ B $ 两点固定两个带电荷量分别为 $ Q_1 $、$ Q_2 $ 的正电荷, 现有一个带正电小球静置于轨道内侧 $ P $ 点(小球可视为点电荷), 已知 $ l_{AP} : l_{BP} = n : 1 $, 则 $ Q_1 : Q_2 $ 是( ).


A.$ 2n^2 : 1 $
B.$ 4n^2 : 1 $
C.$ 2n^3 : 1 $
D.$ 4n^3 : 1 $

答案：
C　解析:设小球带电荷量为q，对小球受力分析如答图8 - 3所示。由正弦定理有$\frac{F_{A}}{\sin\angle CPH}=\frac{F_{B}}{\sin\angle CHP}$，其中$F_{A}=k\frac{Q_{1}q}{l_{AP}^{2}}$，$F_{B}=k\frac{Q_{2}q}{l_{BP}^{2}}$；在$\triangle APO$中有$\frac{l_{AP}}{\sin(\pi - \angle POB)}=\frac{l_{AO}}{\sin\angle APO}$，在$\triangle BPO$中有$\frac{l_{BP}}{\sin\angle POB}=\frac{l_{BO}}{\sin\angle BPO}$；联立解得$Q_{1}:Q_{2}=2n^{3}:1$，选项C正确。