2025年暑假生活北京师范大学出版社高一物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高一物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
知识点一 实验:探究平抛运动的特点
1. 描绘平抛运动轨迹的几种方案
(1)频闪照相法
用频闪照相机记录物体在不同时刻的位置,将这些位置连起来就得到了平抛运动的轨迹. 由于相邻两帧照片间的时间间隔相等,因此只要测出相邻两帧照片间的
(2)喷水法
让持续稳定的细水流水平喷出,在空中形成弯曲的细水柱,它显示了平抛运动的轨迹,设法将它描在纸上就能得到平抛运动的轨迹.
(3)描点法
让小球每次都从斜槽上
2. 判断平抛运动的轨迹是不是抛物线的两种方法
(1)公式法
①原理:若平抛运动的轨迹是抛物线,则以抛出点为坐标原点建立直角坐标系后,轨迹上各点的坐标应满足 $ y = ax^2 $ 的关系( $ a $ 是一个特定常量, $ a \neq 0 $ ).
②验证方法:用刻度尺测量得到几个点的坐标,分别代入 $ y = ax^2 $ 中求出几个不同的常数 $ a $,看在误差允许的范围内这几个不同的常数 $ a $ 是不是趋近于一个常量.
(2)图像法
建立
1. 描绘平抛运动轨迹的几种方案
(1)频闪照相法
用频闪照相机记录物体在不同时刻的位置,将这些位置连起来就得到了平抛运动的轨迹. 由于相邻两帧照片间的时间间隔相等,因此只要测出相邻两帧照片间的
水平距离
,就很容易判断平抛运动在水平方向上的运动特点.(2)喷水法
让持续稳定的细水流水平喷出,在空中形成弯曲的细水柱,它显示了平抛运动的轨迹,设法将它描在纸上就能得到平抛运动的轨迹.
(3)描点法
让小球每次都从斜槽上
同一位置
由静止
滚下,从斜槽末端水平
抛出,用铅笔描出小球经过的位置,通过多次实验,在竖直的背景方格纸上记录小球所经过的多个位置,连起来就得到小球做平抛运动的轨迹.2. 判断平抛运动的轨迹是不是抛物线的两种方法
(1)公式法
①原理:若平抛运动的轨迹是抛物线,则以抛出点为坐标原点建立直角坐标系后,轨迹上各点的坐标应满足 $ y = ax^2 $ 的关系( $ a $ 是一个特定常量, $ a \neq 0 $ ).
②验证方法:用刻度尺测量得到几个点的坐标,分别代入 $ y = ax^2 $ 中求出几个不同的常数 $ a $,看在误差允许的范围内这几个不同的常数 $ a $ 是不是趋近于一个常量.
(2)图像法
建立
$y-x^{2}$
坐标系,根据所测量的各个点的坐标分别计算出对应的 $ y $ 值和 $ x^2 $ 值,在坐标系中描点,连接各点看是否大致在一条直线上
.
答案:
(1)水平距离
(3)同一位置 静止 水平 2.
(2)$y-x^{2}$ 在一条直线上
(1)水平距离
(3)同一位置 静止 水平 2.
(2)$y-x^{2}$ 在一条直线上
知识点二 抛体运动的规律
1. 抛体运动
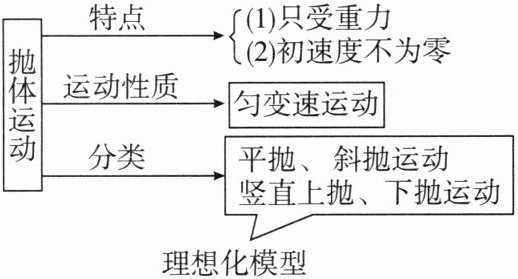
2. 抛体运动的规律
(1)平抛运动的规律

(2)斜抛运动的规律
斜抛运动的分析方法与平抛运动的分析方法相同,即将运动分解为水平方向与竖直方向的两个分运动进行研究,如图 2 - 1.
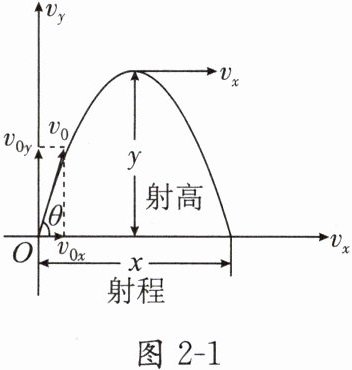
①水平方向: 做匀速直线运动, $ v_x = $
②竖直方向: 做竖直上抛运动或竖直下抛运动, $ v_y = $
1. 抛体运动

2. 抛体运动的规律
(1)平抛运动的规律

(2)斜抛运动的规律
斜抛运动的分析方法与平抛运动的分析方法相同,即将运动分解为水平方向与竖直方向的两个分运动进行研究,如图 2 - 1.

①水平方向: 做匀速直线运动, $ v_x = $
$v_{0}cosθ$
;②竖直方向: 做竖直上抛运动或竖直下抛运动, $ v_y = $
$v_{0}sinθ-gt$
或$v_{0}sinθ+gt$
.
答案:
(1)$v_{0}$ $gt$ $\sqrt {v_{0}^{2}+(gt)^{2}}$ $\frac {gt}{v_{0}}$ $v_{0}t$ $\frac {1}{2}gt^{2}$ $\sqrt {(v_{0}t)^{2}+(\frac {1}{2}gt^{2})^{2}}$ $\frac {gt}{2v_{0}}$ $v_{0}t$ $\frac {1}{2}gt^{2}$
(2)①$v_{0}cosθ$ ②$v_{0}sinθ-gt$ $v_{0}sinθ+gt$
(1)$v_{0}$ $gt$ $\sqrt {v_{0}^{2}+(gt)^{2}}$ $\frac {gt}{v_{0}}$ $v_{0}t$ $\frac {1}{2}gt^{2}$ $\sqrt {(v_{0}t)^{2}+(\frac {1}{2}gt^{2})^{2}}$ $\frac {gt}{2v_{0}}$ $v_{0}t$ $\frac {1}{2}gt^{2}$
(2)①$v_{0}cosθ$ ②$v_{0}sinθ-gt$ $v_{0}sinθ+gt$
查看更多完整答案,请扫码查看


