《2025年暑假综合练习河北人民出版社七年级数学》

9. 如图2-9,已知$AC// DE$,$CE// DF$,CE平分$∠ACB$,求证：DF平分$∠BDE$.

答案： 证明：
∵AC//DE，
∴∠ACB=∠EDB.
∵CE//DF，
∴∠ECB=∠FDB，
∴∠ACE=∠ACB-∠ECB=∠EDB-∠FDB=∠EDF.
∵CE平分∠ACB，
∴∠ACE=∠ECB，
∴∠EDF=∠FDB，
∴DF平分∠BDE.

10. 已知$AB// CD$,$∠ABC与∠BCD$的平分线交于点E,延长BE交CD于点F,过点F作$FG⊥BF$,交直线BC于点G.
(1) 如图2-10①,求证：$EC// FG$；
(2) 如图2-10②,点M在线段BC上,点N在线段FG上,且$∠BEM= ∠MEN$,连接EG. 直接写出一个$∠MEG$的度数,使得$∠NEG= ∠NGE$成立.

答案： （1）证明：
∵AB//CD
∴∠ABC+∠BCD=180°.
∵∠ABC与∠BCD的平分线交于点E，
∴∠BCE=$\frac{1}{2}$∠BCD，∠CBE=$\frac{1}{2}$∠ABC，
∴∠BCE+∠CBE=90°，
∴∠BEC=180°-(∠BCE+∠CBE)=90°.
∵FG⊥BF，
∴∠BEC=∠BFG=90°，
∴EC//FG；（2）∠MEG=45°.

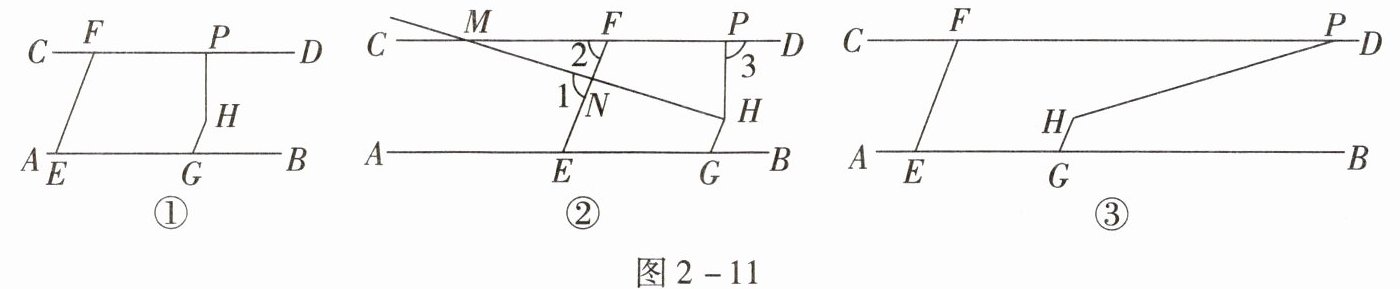
11. 如图2-11①,已知$AB// CD$,$∠BGH= ∠EFC$,点P为直线CD上一动点.
(1) 求证：$EF// GH$；
(2) 作射线HM交直线CD于点M,交直线EF于点N,且$∠GHM= ∠PHM$.
①当点P运动到图2-11②所示的位置时,用等式表示$∠1$,$∠2与∠3$之间的数量关系,并证明；
②当点P运动到图2-11③所示的位置时,补全图形,直接用等式写出$∠HPD$,$∠MFE与∠ENM$之间的数量关系.

答案：
1. （1）证明$EF// GH$：
因为$AB// CD$，根据两直线平行，同位角相等，所以$\angle BGH=\angle GHC$。
又因为$\angle BGH = \angle EFC$，所以$\angle GHC=\angle EFC$。
根据同位角相等，两直线平行，可得$EF// GH$。
2. （2）①$\angle 2=\angle 1+\angle 3$，证明如下：
过点$H$作$HQ// CD$。
因为$EF// GH$，所以$\angle FNH=\angle NHG$（两直线平行，内错角相等）。
因为$HQ// CD$，$EF// CD$，所以$HQ// EF$，则$\angle 2=\angle FNH+\angle QHP$。
又因为$\angle GHM=\angle PHM$，$HQ// CD$，所以$\angle QHP = \angle PHM$，$\angle 1=\angle FNH$（两直线平行，内错角相等）。
所以$\angle 2=\angle 1+\angle 3$。
3. （2）②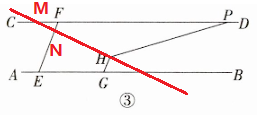，$\angle HPD=\angle MFE+\angle ENM$。
综上，（1）已证明$EF// GH$；（2）①$\angle 2=\angle 1+\angle 3$；②$\angle HPD=\angle MFE+\angle ENM$。