《2025年暑假综合练习河北人民出版社七年级数学》

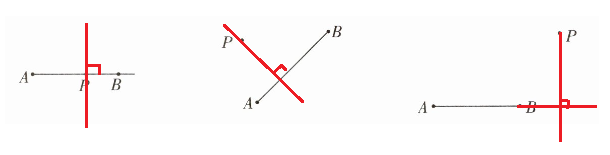
1. 画一条线段或射线的垂线,就是画它们所在直线的垂线. 如图2-1,请你在下面三个图形中,过点P画出射线AB和线段AB的垂线.

答案：

2. 如图2-2,$∠AOB$内有一点P.
(1) 过点P画$PC// OB$交OA于点C,画$PD// OA$交OB于点D；
(2) 写出两对图中互补的角；
(3) 写出两对图中相等的角.

答案： 1. （1）按照平行线的画法完成作图（略）。
2. （2）
因为$PC// OB$，$PD// OA$，根据平行线的性质：
同旁内角互补。
对于$\angle O$与$\angle ODP$，因为$PD// OA$，$\angle O$与$\angle ODP$是同旁内角，所以$\angle O+\angle ODP = 180^{\circ}$；
对于$\angle O$与$\angle OCP$，因为$PC// OB$，$\angle O$与$\angle OCP$是同旁内角，所以$\angle O+\angle OCP = 180^{\circ}$（答案不唯一，还可以是$\angle CPD+\angle ODP = 180^{\circ}$，$\angle CPD+\angle OCP = 180^{\circ}$等）。
3. （3）
根据平行线的性质：
同位角相等，内错角相等。
因为$PC// OB$，所以$\angle CPD=\angle PDO$（内错角相等）；
因为$PD// OA$，所以$\angle CPD=\angle PCO$（内错角相等）（答案不唯一，还可以是$\angle O=\angle CPD$（根据平行四边形的性质，$OCPD$是平行四边形，$\angle O$与$\angle CPD$是平行四边形的一组对角）等）。
综上，（2）答案如$\angle O$与$\angle ODP$，$\angle O$与$\angle OCP$；（3）答案如$\angle CPD=\angle PDO$，$\angle CPD=\angle PCO$。

3. 如图2-3,已知三角形ABC及三角形ABC外一点D,平移三角形ABC,使点A移动到点D,画出平移后的三角形,并保留作图痕迹.

答案： 解：1. 连接AD；
2. 过点B作AD的平行线，在平行线上截取BE=AD，得到点E；
3. 过点C作AD的平行线，在平行线上截取CF=AD，得到点F；
4. 连接DE、EF、FD，三角形DEF即为所求。（作图痕迹保留）

证明：$\because BE平分∠ABC$,CF平分$∠BCD$,
$\therefore ∠ABC= $2∠1,
$∠BCD= $2∠2 (角平分线的性质).
$\because ∠1= ∠2$,
$\therefore ∠ABC= ∠BCD$ (等式的基本性质),
$\therefore AB// CD$ (内错角相等，两直线平行).

答案： 2∠1 2∠2 角平分线的性质 等式的基本性质 内错角相等，两直线平行