《2025年快乐之星暑假篇七年级数学》

【例3】化简与求值：
(1)若$m = - 5$,则代数式$\frac{1}{5}m^{2} + 1$的值为6；
(2)若$m + n = - 5$,则代数式$2m + 2n + 1$的值为-9；
(3)若$5m - 3n = - 5$,请仿照以上求代数式值的方法求出$2(m - n)+4(2m - n)+2$的值.
解：原式$= 10m - 6n + 2 = 2(5m - 3n)+2$.把$5m - 3n = - 5$代入,得原式$= $-8.

答案：

【解析】
(1)把$m = - 5$代入求出即可.

(2)先将$2m + 2n + 1变形为2(m + n)+1$,再把$m + n = - 5$代入求出即可.

【答案】
(1)6
(2) - 9

(3)解：原式$= 10m - 6n + 2 = 2(5m - 3n)+2$.把$5m - 3n = - 5$代入,得原式$= - 8$.

【方法点睛】本题考查求代数式的值,运用了整体代入思想,难度适中.

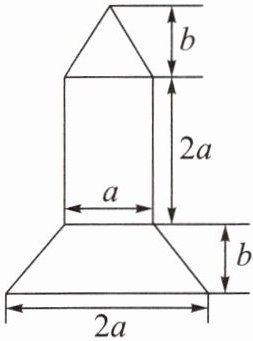
【例4】2022年10月12日,神舟十四号飞行乘组航天员陈冬、刘洋,蔡旭哲进行了“天宫课堂”第三次太空授课,激发了广大青少年对科学的兴趣.七年级同学开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
(1)用式子表示这个截面的面积；
(2)当$a = \frac{5}{2}cm$,$b = 2cm$时,求这个截面的面积.

答案：

【答案】解：
(1)由题意,得$\frac{1}{2}ab + a×2a + \frac{1}{2}(a + 2a)× b = \frac{1}{2}ab + 2a^{2} + \frac{3}{2}ab = 2a^{2} + 2ab$.即这个截面的面积是$2a^{2} + 2ab$.

(2)当$a = \frac{5}{2}cm$,$b = 2cm$时,$2a^{2} + 2ab = 2×(\frac{5}{2})^{2} + 2×\frac{5}{2}×2 = 2×\frac{25}{4} + 10 = 12.5 + 10 = 22.5(cm^{2})$.即这个截面的面积是$22.5cm^{2}$.

【方法点睛】本题主要考查列代数式求值问题,关键是要准确理解题意并正确列式、化简和计算.

1. 下列各式：$-\frac{1}{2}xy$,$0$,$\frac{1}{m}$,$2x + 1$,$\frac{2x - y}{5}$中,整式有(D)
A.1个
B.2个
C.3个
D.4个

答案： D

2. 单项式$- 5x^{2}y$的次数和系数分别是(B)
A.3,5
B.3, - 5
C.2,5
D.2, - 5

答案： B

3. 已知$- 4x^{a}y + x^{2}y^{b} = - 3x^{2}y$,则$a^{2} - b$的值为(C)
A.1
B.2
C.3
D.4

答案： C

4. 一个多项式$M减去多项式- 2x^{2} + 5x - 3$,小马虎同学却误解为加上这个多项式,结果得$x^{3} + 3x + 7$,则多项式$M$是(A)
A.$x^{3} + 2x^{2} - 2x + 10$
B.$- x^{2} + 8x + 4$
C.$3x^{2} - x + 10$
D.$x^{2} - 8x - 4$

答案： A

5. 按照一定规律排列的式子：$\frac{x^{2}}{3}$,$\frac{x^{4}}{5}$,$\frac{x^{6}}{7}$,$\frac{x^{8}}{9}$,…,第7个式子是$\frac{x^{14}}{15}$.

答案： $\frac{x^{14}}{15}$