2025年快乐之星暑假篇七年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐之星暑假篇七年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
【例2】如图,在灯塔O观测小岛B位于南偏西$63^{\circ}$的方向,同时小岛C在灯塔O的北偏东$27^{\circ}$的方向,则$∠BOC$的度数为 (

A.$126^{\circ}$
B.$144^{\circ}$
C.$153^{\circ}$
D.$117^{\circ}$
B
)
A.$126^{\circ}$
B.$144^{\circ}$
C.$153^{\circ}$
D.$117^{\circ}$
答案:
【解析】如图,由题意,得$∠COE= 27^{\circ}$,$∠BOF= 63^{\circ}$,$\therefore ∠BOM= 90^{\circ}-63^{\circ}=27^{\circ}$,$\therefore ∠BOC= ∠BOM+∠MOE+∠COE= 27^{\circ}+90^{\circ}+27^{\circ}=144^{\circ}$.
【答案】B
【方法点睛】本题考查方向角,解题的关键是理解方向角的定义,属于中考常考题型.
【例3】已知点C在直线AB上,$AC= 8cm$,$BC= 6cm$,点M,N分别是AC,BC的中点,求线段MN的长.
答案:
【答案】解:如答图1,当点C在线段AB上时,由点M,N分别是AC,BC的中点,得$MC= \frac{1}{2}AC= 4cm$,$CN= \frac{1}{2}BC= 3cm$. 由线段的和差,得$MN= MC+CN= 7cm$.
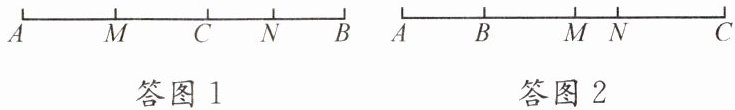
如答图2,当点C在线段AB的延长线上时,由点M,N分别是AC,BC的中点,得$MC= \frac{1}{2}AC= 4cm$,$CN= \frac{1}{2}BC= 3cm$. 由线段的和差,得$MN= MC-CN= 1cm$.
综上所述,线段MN的长是7cm或1cm.
【方法点睛】本题考查了两点的距离,线段中点的性质,线段的和差,分类讨论是解题的关键.
【答案】解:如答图1,当点C在线段AB上时,由点M,N分别是AC,BC的中点,得$MC= \frac{1}{2}AC= 4cm$,$CN= \frac{1}{2}BC= 3cm$. 由线段的和差,得$MN= MC+CN= 7cm$.
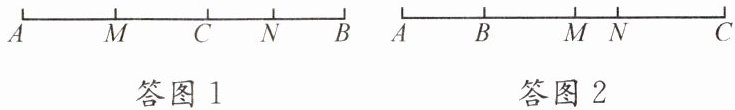
如答图2,当点C在线段AB的延长线上时,由点M,N分别是AC,BC的中点,得$MC= \frac{1}{2}AC= 4cm$,$CN= \frac{1}{2}BC= 3cm$. 由线段的和差,得$MN= MC-CN= 1cm$.
综上所述,线段MN的长是7cm或1cm.
【方法点睛】本题考查了两点的距离,线段中点的性质,线段的和差,分类讨论是解题的关键.
1. 如图是某几何体的表面展开图,则该几何体是 (
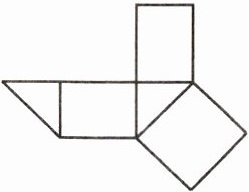
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
B
)
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
答案:
B
2. 如图所示的几何体是由一些正方体组合而成的立体图形,那么从上面看这个几何体得到的平面图形是 (
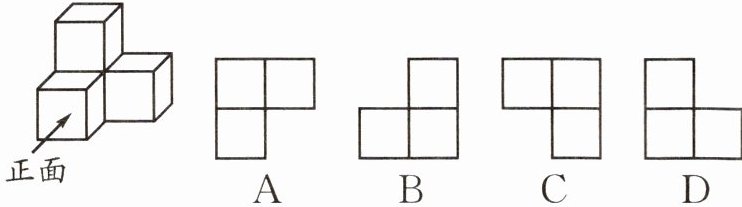
A
)
答案:
A
3. 下列说法:①直线AB和直线BA是同一条直线;②平角是一条直线;③两点之间,线段最短;④若$AB= BC$,则点B是线段AC的中点. 其中正确的有 (
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B
4. 如果一个角的余角等于这个角的补角的$\frac{1}{4}$,那么这个角的度数是 (
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
C
)A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
答案:
【解析】:
设这个角的度数为 $x^{\circ}$。
根据余角的定义,这个角的余角为 $90^{\circ} - x^{\circ}$。
根据补角的定义,这个角的补角为 $180^{\circ} - x^{\circ}$。
根据题意,有方程:
$90^{\circ} - x^{\circ} = \frac{1}{4}(180^{\circ} - x^{\circ})$
展开方程得:
$90^{\circ} - x^{\circ} = 45^{\circ} - \frac{1}{4}x^{\circ}$
整理方程,得:
$\frac{3}{4}x^{\circ} = 45^{\circ}$
解得:
$x = 60^{\circ}$
【答案】:C
设这个角的度数为 $x^{\circ}$。
根据余角的定义,这个角的余角为 $90^{\circ} - x^{\circ}$。
根据补角的定义,这个角的补角为 $180^{\circ} - x^{\circ}$。
根据题意,有方程:
$90^{\circ} - x^{\circ} = \frac{1}{4}(180^{\circ} - x^{\circ})$
展开方程得:
$90^{\circ} - x^{\circ} = 45^{\circ} - \frac{1}{4}x^{\circ}$
整理方程,得:
$\frac{3}{4}x^{\circ} = 45^{\circ}$
解得:
$x = 60^{\circ}$
【答案】:C
5. 如图,已知射线$OA⊥$射线OB,射线OA表示北偏西$20^{\circ}$的方向,则射线OB表示的方向为 (
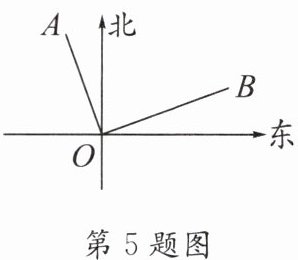
A.北偏东$60^{\circ}$
B.北偏东$55^{\circ}$
C.北偏东$70^{\circ}$
D.东偏北$75^{\circ}$
C
)
A.北偏东$60^{\circ}$
B.北偏东$55^{\circ}$
C.北偏东$70^{\circ}$
D.东偏北$75^{\circ}$
答案:
【解析】:
已知$OA \perp OB$,因此$\angle AOB = 90^\circ$。
射线$OA$表示北偏西$20^\circ$的方向,即从正北方向逆时针转$20^\circ$到达$OA$。
由于$OA$与$OB$垂直,从$OA$顺时针转$90^\circ$到达$OB$。
因此,从正北方向顺时针转$90^\circ - 20^\circ = 70^\circ$到达$OB$。
所以,射线$OB$表示的方向为北偏东$70^\circ$。
【答案】:C.北偏东$70^\circ$
已知$OA \perp OB$,因此$\angle AOB = 90^\circ$。
射线$OA$表示北偏西$20^\circ$的方向,即从正北方向逆时针转$20^\circ$到达$OA$。
由于$OA$与$OB$垂直,从$OA$顺时针转$90^\circ$到达$OB$。
因此,从正北方向顺时针转$90^\circ - 20^\circ = 70^\circ$到达$OB$。
所以,射线$OB$表示的方向为北偏东$70^\circ$。
【答案】:C.北偏东$70^\circ$
查看更多完整答案,请扫码查看


