第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
11.已知小明步行的时间为$10min$,步长为$0.5m$,步数为$1200$。
(1)求小明步行的平均速度。
(2)若以该速度再沿直线步行$1km$,求小明所需要的时间。
(1)求小明步行的平均速度。
(2)若以该速度再沿直线步行$1km$,求小明所需要的时间。
答案:
解析:
(1)由题意可知,小明行走的路程s=1 200×0.5 m=600 m,小明步行的平均速度v=$\frac{s}{t}$=$\frac{600\ m}{10×60\ s}$=1 m/s。
(2)若以该速度再沿直线步行1 km,小明所需要的时间t₁=$\frac{s₁}{v}$=$\frac{1000\ m}{1\ m/s}$=1 000 s。答案:
(1)1 m/s
(2)1 000 s
(1)由题意可知,小明行走的路程s=1 200×0.5 m=600 m,小明步行的平均速度v=$\frac{s}{t}$=$\frac{600\ m}{10×60\ s}$=1 m/s。
(2)若以该速度再沿直线步行1 km,小明所需要的时间t₁=$\frac{s₁}{v}$=$\frac{1000\ m}{1\ m/s}$=1 000 s。答案:
(1)1 m/s
(2)1 000 s
12.长度为$20m的列车以36km/h的速度匀速通过一座长度为40m$的铁桥。
(1)该列车全部通过铁桥需要多长时间?
(2)该列车全部在铁桥上的时间是多少?
(1)该列车全部通过铁桥需要多长时间?
(2)该列车全部在铁桥上的时间是多少?
答案:
解析:
(1)由题意知,该列车全部通过铁桥行驶的路程s=L$_{车}$+L$_{桥}$=20 m+40 m=60 m,已知列车的速度v=36 km/h=10 m/s,由v=$\frac{s}{t}$可得,该列车全部通过铁桥需要的时间t=$\frac{s}{v}$=$\frac{60\ m}{10\ m/s}$=6 s。
(2)该列车全部在铁桥上行驶的路程s'=L$_{桥}$-L$_{车}$=40 m-20 m=20 m,则该列车全部在铁桥上的时间t'=$\frac{s'}{v}$=$\frac{20\ m}{10\ m/s}$=2 s。答案:
(1)6 s
(2)2 s
(1)由题意知,该列车全部通过铁桥行驶的路程s=L$_{车}$+L$_{桥}$=20 m+40 m=60 m,已知列车的速度v=36 km/h=10 m/s,由v=$\frac{s}{t}$可得,该列车全部通过铁桥需要的时间t=$\frac{s}{v}$=$\frac{60\ m}{10\ m/s}$=6 s。
(2)该列车全部在铁桥上行驶的路程s'=L$_{桥}$-L$_{车}$=40 m-20 m=20 m,则该列车全部在铁桥上的时间t'=$\frac{s'}{v}$=$\frac{20\ m}{10\ m/s}$=2 s。答案:
(1)6 s
(2)2 s
13.一列长度为$150m$的火车匀速行驶,一名观察者站在路基旁测出整列火车通过他用时$5s$。
(1)这列火车的速度是多少?
(2)已知$A地与B地相距54km$,如果这列火车以上述速度匀速行驶,火车从$A地到B$地需用多少小时?
(3)如果火车以这个速度完全通过一条隧道需要$1min$,则这条隧道长多少?
(1)这列火车的速度是多少?
(2)已知$A地与B地相距54km$,如果这列火车以上述速度匀速行驶,火车从$A地到B$地需用多少小时?
(3)如果火车以这个速度完全通过一条隧道需要$1min$,则这条隧道长多少?
答案:
解析:
(1)由题意可知,火车在5 s内通过的路程是150 m(即等于火车的长度),则这列火车行驶的速度v=$\frac{s₁}{t₁}$=$\frac{150\ m}{5\ s}$=30 m/s=108 km/h。
(2)由v=$\frac{s}{t}$得,火车从A地到B地需用时间t₂=$\frac{s₂}{v}$=$\frac{54\ km}{108\ km/h}$=0.5 h。
(3)由v=$\frac{s}{t}$得,火车1 min通过的路程s₃=vt₃=30 m/s×1×60 s=1 800 m,则这条隧道长L$_{隧道}$=s₃-L$_{车}$=1 800 m-150 m=1 650 m。答案:
(1)108 km/h
(2)0.5 h
(3)1 650 m
(1)由题意可知,火车在5 s内通过的路程是150 m(即等于火车的长度),则这列火车行驶的速度v=$\frac{s₁}{t₁}$=$\frac{150\ m}{5\ s}$=30 m/s=108 km/h。
(2)由v=$\frac{s}{t}$得,火车从A地到B地需用时间t₂=$\frac{s₂}{v}$=$\frac{54\ km}{108\ km/h}$=0.5 h。
(3)由v=$\frac{s}{t}$得,火车1 min通过的路程s₃=vt₃=30 m/s×1×60 s=1 800 m,则这条隧道长L$_{隧道}$=s₃-L$_{车}$=1 800 m-150 m=1 650 m。答案:
(1)108 km/h
(2)0.5 h
(3)1 650 m
14.高速公路$ETC$收费系统是对过往车辆无须停车即能实现收费的电子系统。如图所示是某高速公路入口处的$ETC$通道示意图。现有一辆汽车在某高速路上以$25m/s的速度匀速行驶20min$后到达收费站,在进入$ETC收费岛区域前s_1 = 50m$处开始减速,经$t_1 = 4s后行驶至ETC$收费岛边界,然后再以$5m/s的速度匀速通过长度s_2 = 25m的ETC$收费岛,已知车的长度$s_3 = 5m$。求:
(1)汽车到达收费站前匀速行驶的路程$s$;
(2)汽车完全通过$ETC收费岛所用的时间t_2$;
(3)汽车从减速开始到离开$ETC收费岛全过程的平均速度v$。
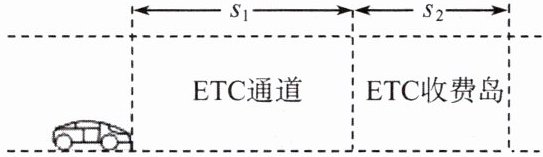
(1)汽车到达收费站前匀速行驶的路程$s$;
(2)汽车完全通过$ETC收费岛所用的时间t_2$;
(3)汽车从减速开始到离开$ETC收费岛全过程的平均速度v$。

答案:
解析:
(1)汽车在高速公路上的速度v$_{高速}$=25 m/s=90 km/h,所用时间t$_{高速}$=20 min=$\frac{1}{3}$ h。由v=$\frac{s}{t}$可得,汽车到达收费站前匀速行驶的路程s=v$_{高速}$t$_{高速}$=90 km/h×$\frac{1}{3}$ h=30 km。
(2)由题意可知,汽车以5 m/s的速度匀速通过ETC收费岛的路程s'=s₂+s₃=25 m+5 m=30 m,由v=$\frac{s}{t}$可得,汽车完全通过ETC收费岛所用的时间t₂=$\frac{s'}{v'}$=$\frac{30\ m}{5\ m/s}$=6 s。
(3)汽车从减速开始到离开ETC收费岛全过程的总路程s$_{总}$=s₁+s₂+s₃=50 m+25 m+5 m=80 m,从减速开始到离开ETC收费岛全过程的总时间t$_{总}$=t₁+t₂=4 s+6 s=10 s,则汽车从减速开始到离开ETC收费岛全过程的平均速度v=$\frac{s_{总}}{t_{总}}$=$\frac{80\ m}{10\ s}$=8 m/s。答案:
(1)30 km
(2)6 s
(3)8 m/s
(1)汽车在高速公路上的速度v$_{高速}$=25 m/s=90 km/h,所用时间t$_{高速}$=20 min=$\frac{1}{3}$ h。由v=$\frac{s}{t}$可得,汽车到达收费站前匀速行驶的路程s=v$_{高速}$t$_{高速}$=90 km/h×$\frac{1}{3}$ h=30 km。
(2)由题意可知,汽车以5 m/s的速度匀速通过ETC收费岛的路程s'=s₂+s₃=25 m+5 m=30 m,由v=$\frac{s}{t}$可得,汽车完全通过ETC收费岛所用的时间t₂=$\frac{s'}{v'}$=$\frac{30\ m}{5\ m/s}$=6 s。
(3)汽车从减速开始到离开ETC收费岛全过程的总路程s$_{总}$=s₁+s₂+s₃=50 m+25 m+5 m=80 m,从减速开始到离开ETC收费岛全过程的总时间t$_{总}$=t₁+t₂=4 s+6 s=10 s,则汽车从减速开始到离开ETC收费岛全过程的平均速度v=$\frac{s_{总}}{t_{总}}$=$\frac{80\ m}{10\ s}$=8 m/s。答案:
(1)30 km
(2)6 s
(3)8 m/s
查看更多完整答案,请扫码查看


