3. 绿色环保已成为人们生活中重要的理念,很多乡镇家庭用上了清洁干净的液化天然气,已知水的比热容$c= 4.2× 10^{3}\ J/(kg·℃)$,天然气的热值$q= 4.2× 10^{7}\ J/m^{3}$。求:
(1)将4 kg初温为25 ℃的水加热到100 ℃,水吸收的热量。
(2)若完全燃烧天然气放出的热量有40%被水吸收,加热这些水需要燃烧天然气的体积。
(1)将4 kg初温为25 ℃的水加热到100 ℃,水吸收的热量。
(2)若完全燃烧天然气放出的热量有40%被水吸收,加热这些水需要燃烧天然气的体积。
答案:
【解析】:
这道题目主要考查热量计算公式和热效率的应用。
对于第一问,需要用到热量计算公式$Q = cm\Delta t$来计算水吸收的热量,其中$c$是水的比热容,$m$是水的质量,$\Delta t$是水的温度变化。
对于第二问,需要用到热效率公式和天然气热值的定义来计算需要燃烧的天然气体积。热效率是指被水吸收的热量与天然气完全燃烧放出的热量之比,天然气的热值是指单位体积天然气完全燃烧放出的热量。
【答案】:
(1)解:水吸收的热量可以根据公式$Q_{吸} = cm\Delta t$计算,
代入已知数值:$c = 4.2 × 10^{3} J/(kg \cdot ^{\circ}C)$,$m = 4kg$,$\Delta t = 100 - 25 = 75^{\circ}C$,
得到:$Q_{吸} = 4.2 × 10^{3} × 4 × 75 = 1.26 × 10^{6}J$;
答:水吸收的热量为$1.26 × 10^{6}J$;
(2)解:由$\eta = \frac{Q_{吸}}{Q_{放}}$得,
天然气完全燃烧放出的热量为:$Q_{放} = \frac{Q_{吸}}{\eta} = \frac{1.26 × 10^{6}}{40\%} = 3.15 × 10^{6}J$,
由$Q_{放} = Vq$得,需要燃烧的天然气的体积为:$V = \frac{Q_{放}}{q} = \frac{3.15 × 10^{6}}{4.2 × 10^{7}} = 0.075m^{3}$;
答:需要燃烧$0.075m^{3}$的天然气。
这道题目主要考查热量计算公式和热效率的应用。
对于第一问,需要用到热量计算公式$Q = cm\Delta t$来计算水吸收的热量,其中$c$是水的比热容,$m$是水的质量,$\Delta t$是水的温度变化。
对于第二问,需要用到热效率公式和天然气热值的定义来计算需要燃烧的天然气体积。热效率是指被水吸收的热量与天然气完全燃烧放出的热量之比,天然气的热值是指单位体积天然气完全燃烧放出的热量。
【答案】:
(1)解:水吸收的热量可以根据公式$Q_{吸} = cm\Delta t$计算,
代入已知数值:$c = 4.2 × 10^{3} J/(kg \cdot ^{\circ}C)$,$m = 4kg$,$\Delta t = 100 - 25 = 75^{\circ}C$,
得到:$Q_{吸} = 4.2 × 10^{3} × 4 × 75 = 1.26 × 10^{6}J$;
答:水吸收的热量为$1.26 × 10^{6}J$;
(2)解:由$\eta = \frac{Q_{吸}}{Q_{放}}$得,
天然气完全燃烧放出的热量为:$Q_{放} = \frac{Q_{吸}}{\eta} = \frac{1.26 × 10^{6}}{40\%} = 3.15 × 10^{6}J$,
由$Q_{放} = Vq$得,需要燃烧的天然气的体积为:$V = \frac{Q_{放}}{q} = \frac{3.15 × 10^{6}}{4.2 × 10^{7}} = 0.075m^{3}$;
答:需要燃烧$0.075m^{3}$的天然气。
4. 2024年11月12日,第十五届中国航展在珠海开幕。下图是我国自主研制的大型水陆两栖飞机“鲲龙”号,具备强大的灭火救援能力,是国家应急救援体系建设必备的重大航空装备。航展上,“鲲龙”号飞机飞行表演1000 s,消耗航空燃油900 kg,发动机的平均功率为$1.8× 10^{7}\ W$。已知$q_{航空燃油}= 4× 10^{7}\ J/kg$,求:
(1)发动机做的有用功。
(2)消耗的航空燃油完全燃烧放出的热量。
(3)发动机的效率。

(1)发动机做的有用功。
(2)消耗的航空燃油完全燃烧放出的热量。
(3)发动机的效率。

答案:
解:
(1)发动机做的有用功:
由$P = \frac{W}{t}$得,$W = Pt = 1.8×10^{7}\ W×1000\ s = 1.8×10^{10}\ J$。
(2)消耗的航空燃油完全燃烧放出的热量:
$Q_{放} = mq_{航空燃油} = 900\ kg×4×10^{7}\ J/kg = 3.6×10^{10}\ J$。
(3)发动机的效率:
$\eta = \frac{W}{Q_{放}}×100\% = \frac{1.8×10^{10}\ J}{3.6×10^{10}\ J}×100\% = 50\%$。
答:
(1)发动机做的有用功为$1.8×10^{10}\ J$;
(2)消耗的航空燃油完全燃烧放出的热量为$3.6×10^{10}\ J$;
(3)发动机的效率为$50\%$。
(1)发动机做的有用功:
由$P = \frac{W}{t}$得,$W = Pt = 1.8×10^{7}\ W×1000\ s = 1.8×10^{10}\ J$。
(2)消耗的航空燃油完全燃烧放出的热量:
$Q_{放} = mq_{航空燃油} = 900\ kg×4×10^{7}\ J/kg = 3.6×10^{10}\ J$。
(3)发动机的效率:
$\eta = \frac{W}{Q_{放}}×100\% = \frac{1.8×10^{10}\ J}{3.6×10^{10}\ J}×100\% = 50\%$。
答:
(1)发动机做的有用功为$1.8×10^{10}\ J$;
(2)消耗的航空燃油完全燃烧放出的热量为$3.6×10^{10}\ J$;
(3)发动机的效率为$50\%$。
5. 小明为了控制灯泡的亮度,设计了如图所示的电路,已知电源电压恒定不变,灯泡L正常发光的电压为3 V,且灯泡电阻不随温度变化。将滑片P置于a端,闭合开关S,缓慢移动滑片P,当滑片P位于b端时,电流表示数为0.6 A,灯泡恰好正常发光。求:
(1)电源电压U。
(2)灯泡L的电阻。
(3)当电流表的示数为0.2 A时,此时滑动变阻器接入电路的电阻。
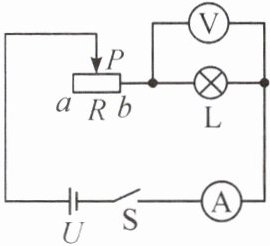
(1)电源电压U。
(2)灯泡L的电阻。
(3)当电流表的示数为0.2 A时,此时滑动变阻器接入电路的电阻。

答案:
【解析】:
本题主要考查了欧姆定律和串联电路的特点,包括电源电压的计算、灯泡电阻的求解以及滑动变阻器接入电路电阻的计算。
(1)当滑片P位于b端时,电路为灯泡L的简单电路,此时灯泡正常发光,说明灯泡两端的电压等于其额定电压,即电源电压$U = U_{L} = 3V$。
(2)根据欧姆定律$I = \frac{U}{R}$,可以求出灯泡L的电阻$R_{L} = \frac{U_{L}}{I_{L}}$。由于灯泡正常发光时电流为$0.6A$,所以$R_{L} = \frac{3V}{0.6A} = 5\Omega$。
(3)当电流表的示数为$0.2A$时,根据欧姆定律求出电路中的总电阻$R_{总} = \frac{U}{I} = \frac{3V}{0.2A} = 15\Omega$。由于串联电路中总电阻等于各分电阻之和,所以滑动变阻器接入电路的电阻$R = R_{总} - R_{L} = 15\Omega - 5\Omega = 10\Omega$。
【答案】:
(1)电源电压$U = 3V$;
(2)灯泡L的电阻$R_{L} = 5\Omega$;
(3)当电流表的示数为$0.2A$时,滑动变阻器接入电路的电阻$R = 10\Omega$。
本题主要考查了欧姆定律和串联电路的特点,包括电源电压的计算、灯泡电阻的求解以及滑动变阻器接入电路电阻的计算。
(1)当滑片P位于b端时,电路为灯泡L的简单电路,此时灯泡正常发光,说明灯泡两端的电压等于其额定电压,即电源电压$U = U_{L} = 3V$。
(2)根据欧姆定律$I = \frac{U}{R}$,可以求出灯泡L的电阻$R_{L} = \frac{U_{L}}{I_{L}}$。由于灯泡正常发光时电流为$0.6A$,所以$R_{L} = \frac{3V}{0.6A} = 5\Omega$。
(3)当电流表的示数为$0.2A$时,根据欧姆定律求出电路中的总电阻$R_{总} = \frac{U}{I} = \frac{3V}{0.2A} = 15\Omega$。由于串联电路中总电阻等于各分电阻之和,所以滑动变阻器接入电路的电阻$R = R_{总} - R_{L} = 15\Omega - 5\Omega = 10\Omega$。
【答案】:
(1)电源电压$U = 3V$;
(2)灯泡L的电阻$R_{L} = 5\Omega$;
(3)当电流表的示数为$0.2A$时,滑动变阻器接入电路的电阻$R = 10\Omega$。
查看更多完整答案,请扫码查看


