第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
4. 一袋食用盐标准净含量是225克,检查员抽检了5袋,并将数据记录在表中:
| |第1袋|第2袋|第3袋|第4袋|第5袋|
|比标准净含量多的克数|-1|+2|+3|-5|-2|
(1)第1袋食用盐的净含量是(
(2)第3袋食用盐比第2袋食用盐重(
(3)这5袋食用盐的总净含量是多少克?
| |第1袋|第2袋|第3袋|第4袋|第5袋|
|比标准净含量多的克数|-1|+2|+3|-5|-2|
(1)第1袋食用盐的净含量是(
224
)克。(2)第3袋食用盐比第2袋食用盐重(
1
)克,比第4袋食用盐重(8
)克。(3)这5袋食用盐的总净含量是多少克?
225×5-1+2+3-5-2=1122(克)
答案:
(1)224
(2)1 8
(3)225×5-1+2+3-5-2=1122(克)
(1)224
(2)1 8
(3)225×5-1+2+3-5-2=1122(克)
5. 用1、5、8、0这四个数字和小数点按要求写一个数(每个数字都用)。
(1)最小的三位小数:(
(2)最大的两位小数:(
(3)最大的一位小数:(
(4)读出一个零的最小的两位小数:(
(5)不需要读出零的最大的两位小数:(
(1)最小的三位小数:(
0.158
)。(2)最大的两位小数:(
85.10
)。(3)最大的一位小数:(
851.0
)。(4)读出一个零的最小的两位小数:(
15.08
)。(5)不需要读出零的最大的两位小数:(
80.51
)。
答案:
(1)0.158
(2)85.10
(3)851.0
(4)15.08
(5)80.51
(1)0.158
(2)85.10
(3)851.0
(4)15.08
(5)80.51
(1)
|1|2|3|4|5|…|m|…|
|1|4|9|16|25|…|
|3|5|7|9|11|…|
(2)小明按一定的规律写数:1,2,-3,4,5,-6,7,8,-9,…,当写完第200个数时他停了下来。他写的数中一共有(
(3)请仔细观察下面的图形,根据正方形的个数与直角三角形个数的关系把下表填写完整。
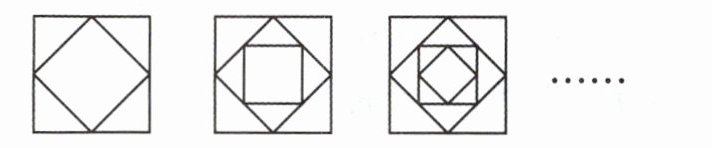
|正方形个数|2|3|4|…|
|直角三角形个数|4|8|
(4)豆豆用蓝白两种方块照下图这样拼图。

第n个图中蓝方块有(
|1|2|3|4|5|…|m|…|
|1|4|9|16|25|…|
m²
|…||3|5|7|9|11|…|
2m+1
|…|(2)小明按一定的规律写数:1,2,-3,4,5,-6,7,8,-9,…,当写完第200个数时他停了下来。他写的数中一共有(
134
)个正数,(66
)个负数。(3)请仔细观察下面的图形,根据正方形的个数与直角三角形个数的关系把下表填写完整。

|正方形个数|2|3|4|…|
26
|…|a||直角三角形个数|4|8|
12
|…|100|…|4(a-1)
|(4)豆豆用蓝白两种方块照下图这样拼图。

第n个图中蓝方块有(
2+2n
)个;豆豆拼成的一个图中有47个白方块,这个图是第(15
)个图。
答案:
(1)$m^{2}$ 2m+1
(2)134 66
(3)12 26 4(a-1)
(4)2+2n 15 提示:
(1)按规律填表即可。
(2)通过观察发现,可将这些数每3个分为一组,即(1,2,-3),(4,5,-6),(7,8,-9)……由此可以发现,每组中有两个正数,一个负数,并且负数是每组中的最后一个数,根据此规律即可求出小明写的这200个数中正数、负数的个数。200÷3=66(组)……2(个),正数共有66×2+2=134(个),负数有200-134=66(个)。
(3)直角三角形个数=(正方形个数-1)×4。
(4)每个题图中最左边的2个蓝方块是固定不变的。第①个题图中,蓝方块有4个,可以看成是由“2+2×1”得到的;第②个题图中,蓝方块有6个,可以看成是由“2+2×2”得到的……所以第n个题图中,蓝方块有(2+2n)个。每个题图中左右各1个白方块是固定不变的,第①个题图中,白方块有5个,可以看成是由“2+1×3”得到的;第②个题图中,白方块有8个,可以看成是由“2+2×3”得到的……所以第n个题图中,白方块有(2+3n)个,所以n=(白方块的个数-2)÷3。
(1)$m^{2}$ 2m+1
(2)134 66
(3)12 26 4(a-1)
(4)2+2n 15 提示:
(1)按规律填表即可。
(2)通过观察发现,可将这些数每3个分为一组,即(1,2,-3),(4,5,-6),(7,8,-9)……由此可以发现,每组中有两个正数,一个负数,并且负数是每组中的最后一个数,根据此规律即可求出小明写的这200个数中正数、负数的个数。200÷3=66(组)……2(个),正数共有66×2+2=134(个),负数有200-134=66(个)。
(3)直角三角形个数=(正方形个数-1)×4。
(4)每个题图中最左边的2个蓝方块是固定不变的。第①个题图中,蓝方块有4个,可以看成是由“2+2×1”得到的;第②个题图中,蓝方块有6个,可以看成是由“2+2×2”得到的……所以第n个题图中,蓝方块有(2+2n)个。每个题图中左右各1个白方块是固定不变的,第①个题图中,白方块有5个,可以看成是由“2+1×3”得到的;第②个题图中,白方块有8个,可以看成是由“2+2×3”得到的……所以第n个题图中,白方块有(2+3n)个,所以n=(白方块的个数-2)÷3。
7. 假设思想猜谜比赛中,规定每人回答10题,答对1题得5分,答错1题或不答得-3分。明明每道题都答了,共得26分,他答对了几道题?
答案:
5×10=50(分) (50-26)÷(5+3)=3(道) 10-3=7(道) 提示:假设全部答对得5×10=50(分)。答错1题或不答,不仅5分得不到,还要减3分,相当于错1题,就从50分里减去8分。明明得了26分,比满分50分少了50-26=24(分),用24÷8求出答错或不答的有3题。所以明明答对了10-3=7(道)题。
查看更多完整答案,请扫码查看


